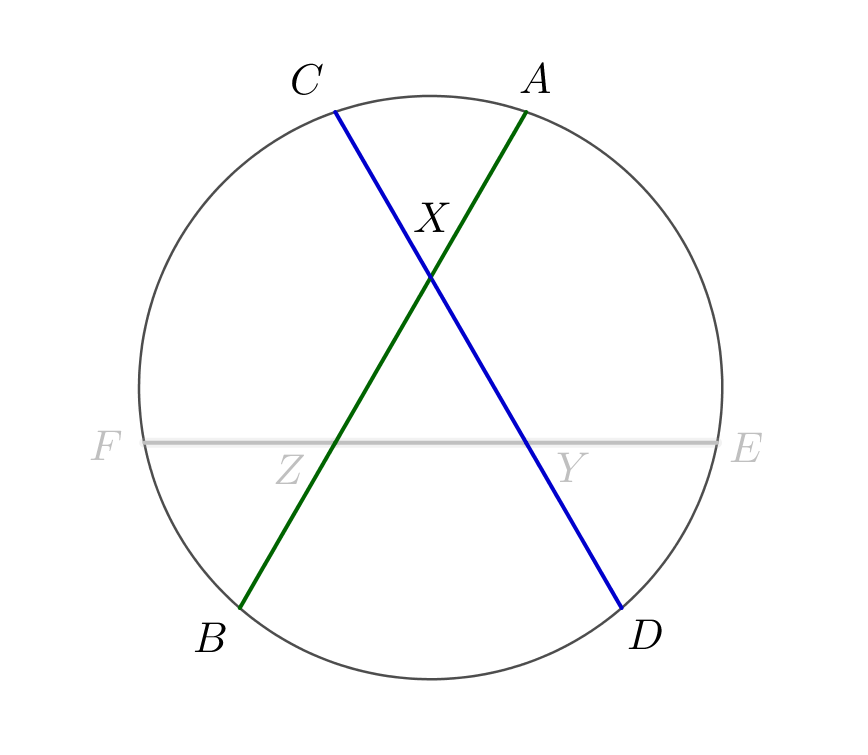
В окружности проведены три попарно пересекающиеся хорды. Каждая хорда делится точкой пересечения на три равные части. Найдите радиус окружности, если одна из хорд равна \(\displaystyle a\small.\)
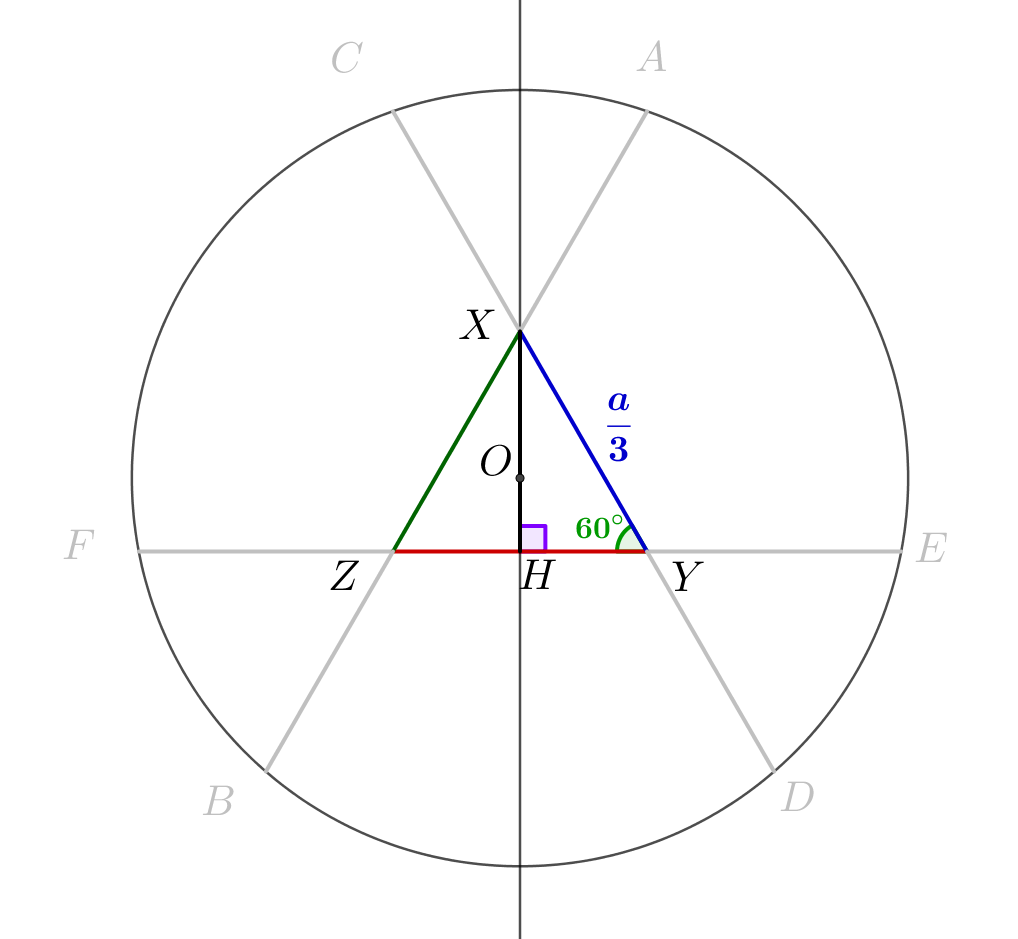
Каждая хорда делится точкой пересечения в одинаковом отношении \(\displaystyle 1:2\small.\)
Центр окружности лежит на серединном перпендикуляре к каждой из хорд. Тогда центр окружности является также центром треугольника \(\displaystyle XYZ\small.\) Опустим перпендикуляр \(\displaystyle OH\) на \(\displaystyle ZY\small.\) |  |
\(\displaystyle OH=\frac{1}{3}\cdot\frac{a}{3}\cdot\frac{\sqrt{3}}{2}=\frac{a\sqrt{3}}{18}\small.\)
Рассмотрим треугольник \(\displaystyle OHE\small.\) Он прямоугольный и его катеты \(\displaystyle OH=\frac{a\sqrt{3}}{18}\) и \(\displaystyle EH=\frac{a}{2}\small.\) Тогда по теореме Пифагора найдем его гипотенузу: \(\displaystyle OE^2=OH^2+EH^2=\left(\frac{a\sqrt{3}}{18}\right)^2+\left(\frac{a}{2}\right)^2=\frac{7a^2}{27}\small,\) \(\displaystyle OE=\frac{a\sqrt{7}}{3\sqrt{3}}\small.\) Отрезок \(\displaystyle OE\) является радиусом окружности. | 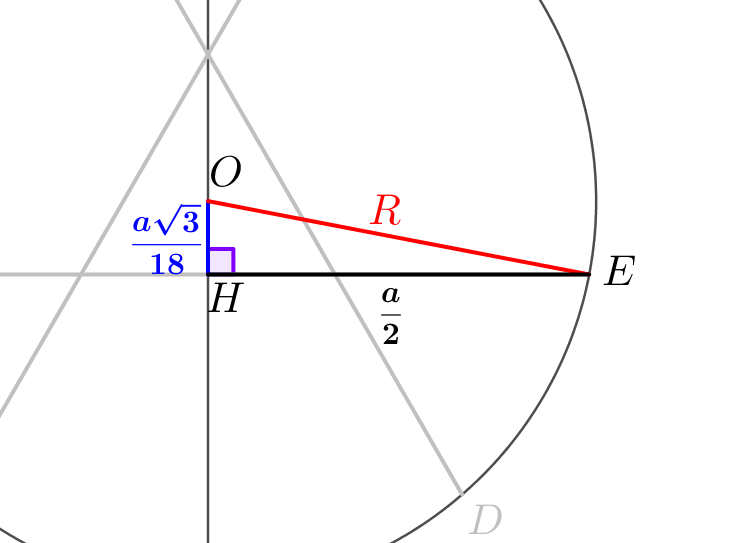 |
Ответ: \(\displaystyle \frac{\sqrt{7}a}{3\sqrt{3}}\small.\)