Хорда \(\displaystyle AB\) стягивает дугу окружности, равную \(\displaystyle 120^{\circ}\small.\) На этой дуге выбрали точку \(\displaystyle C\small,\) а на хорде \(\displaystyle AB\) выбрали точку \(\displaystyle D\small.\) При этом \(\displaystyle AD=4,\,BD=2,\,DC=2\sqrt{2}\small.\) Найдите площадь треугольника \(\displaystyle ABC\small.\)
\(\displaystyle \color{red}{S_{ABC}\,–\,\small?}\) | 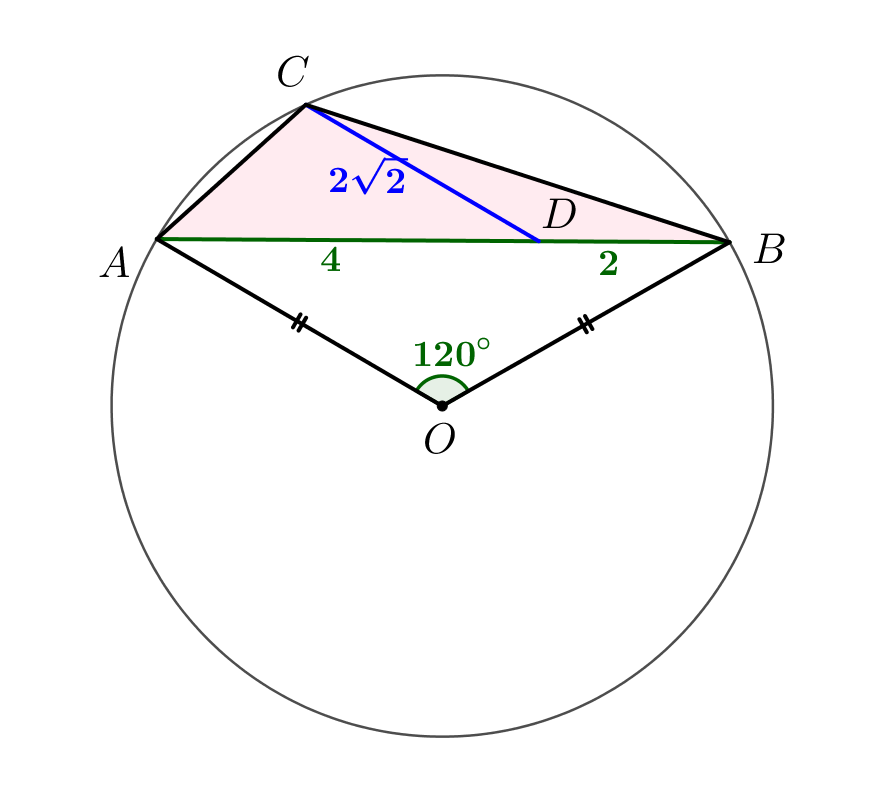 |
Чтобы решить задачу:
- найдем радиус окружности,
- найдем расстояние от точки \(\displaystyle D\) до центра окружности,
- найдем высоту треугольника \(\displaystyle ABC\small.\)
\(\displaystyle R=2\sqrt{3}\small.\)
Рассмотрим треугольник \(\displaystyle ABO\small.\) Центральный угол \(\displaystyle AOB\) опирается на дугу \(\displaystyle 120^{\circ}\small,\) то есть \(\displaystyle \angle AOB=120^{\circ}\small.\) Треугольник \(\displaystyle AOB\) равнобедренный, так как радиусы равны: \(\displaystyle AO=BO\small.\) Тогда \(\displaystyle \angle ABO=\angle BAO=(180^{\circ}-120^{\circ}):2=30^{\circ}\small.\) Проведем высоту \(\displaystyle OH\) треугольника \(\displaystyle AOB\small.\) Поскольку треугольник \(\displaystyle AOB\) равнобедренный, то \(\displaystyle H\) еще середина стороны: \(\displaystyle AH=BH=\frac{AB}{2}=\frac{4+2}{2}=3\small.\) Следовательно, в прямоугольном треугольнике \(\displaystyle AHO{\small:}\) \(\displaystyle AO=\frac{AH}{\cos30^{\circ}}=3:\frac{\sqrt{3}}{2}=2\sqrt{3}\small.\) | 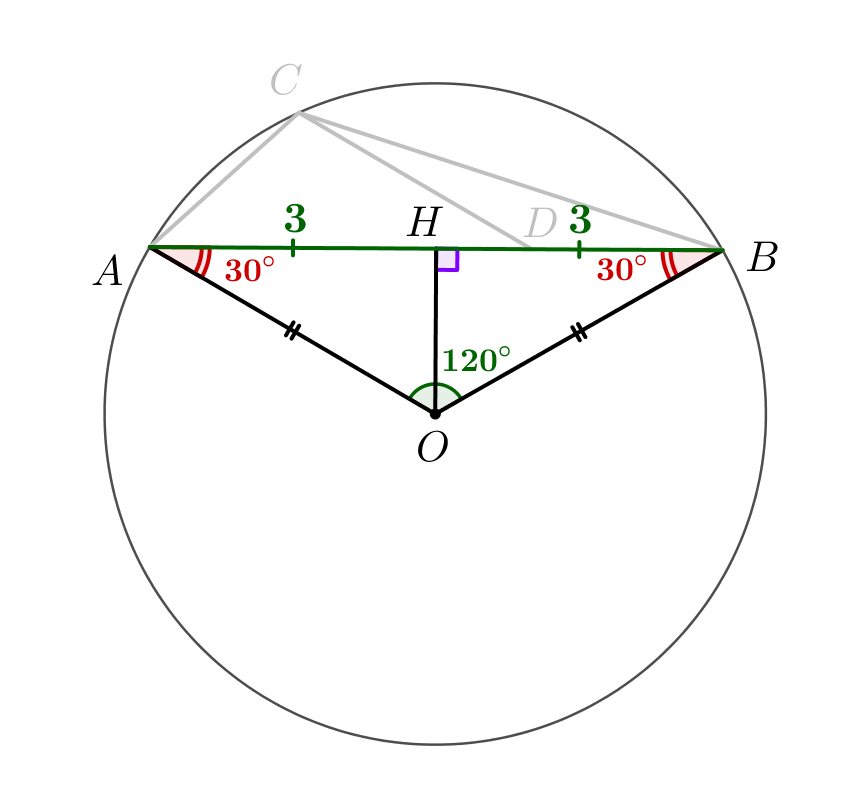 |
\(\displaystyle OD=2\small.\)
Через точку \(\displaystyle D\) проходят хорды \(\displaystyle AB\) и \(\displaystyle CE\small.\) Произведение отрезков пересекающихся хорд равны. Тогда \(\displaystyle AD\cdot BD=CD\cdot DE\small.\) Подставляя известные значения \(\displaystyle AD=4,\,BD=2,\,CD=2\sqrt{2}\small,\) получаем \(\displaystyle 4\cdot2=2\sqrt{2}\cdot DE\small,\) \(\displaystyle DE=\frac{4\cdot2}{2\sqrt{2}}=2\sqrt{2}\small.\) | 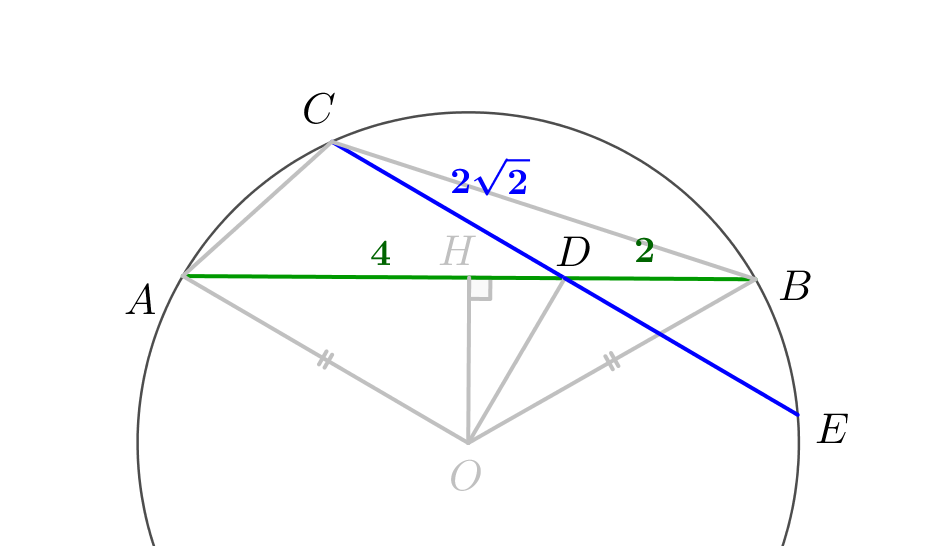 |
То есть \(\displaystyle D\)– середина хорды \(\displaystyle CE\small.\) Прямая, проходящая через центр окружности и середину хорды, перпендикулярна этой хорде. То есть \(\displaystyle \angle ODC=90^{\circ}\small.\) В прямоугольном треугольнике \(\displaystyle CDO\) один из катетов \(\displaystyle CD=2\sqrt{2}\) и гипотенуза \(\displaystyle CO=R=2\sqrt{3}\small.\) Тогда по теореме Пифагора оставшийся катет: \(\displaystyle OD^2=CO^2-CD^2=\left(2\sqrt{3}\right)^2-\left(2\sqrt{2}\right)^2=4\small,\) \(\displaystyle DO=\sqrt{4}=2\small.\) | 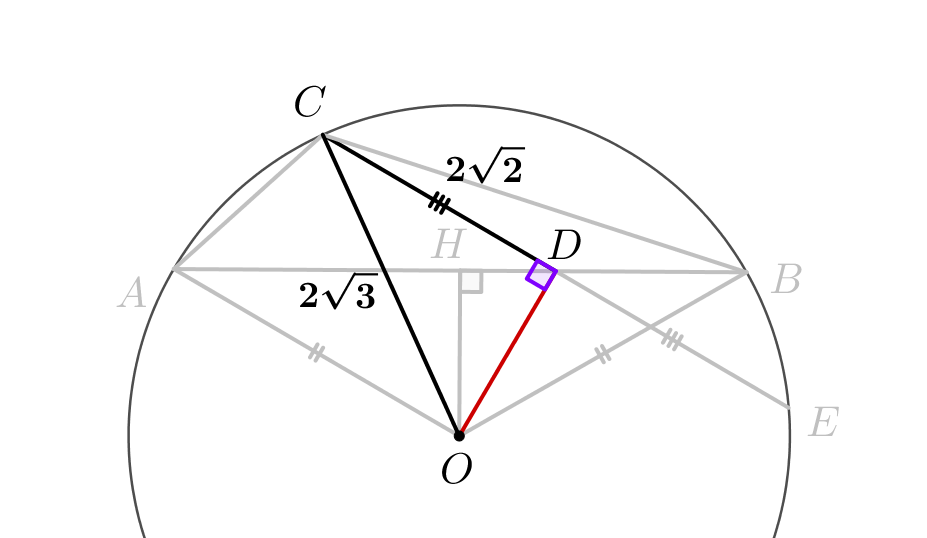 |
\(\displaystyle CK=\sqrt{2}\small.\)
Проведем \(\displaystyle CK\) – высоту треугольника \(\displaystyle ABC{\small.}\) Найдем угол \(\displaystyle CDK\small.\) Поскольку \(\displaystyle BD=OD=2{ \small ,}\)то треугольник \(\displaystyle DBO\) равнобедренный и \(\displaystyle \angle DOB=\angle DBO=30^{\circ}\small.\) Внешний угол этого треугольника \(\displaystyle \angle ADO=30^{\circ}+30^{\circ}=60^{\circ}\small.\) Поскольку \(\displaystyle \angle CDO=90^{\circ}\small,\) то \(\displaystyle \angle ADC=\angle CDO-\angle ADO=90^{\circ}-60^{\circ}=30^{\circ}\small.\) Тогда в прямоугольном треугольнике \(\displaystyle CDK\) острые углы \(\displaystyle 30^{\circ},\,60^{\circ}\small.\) В таком прямоугольном треугольнике сторона, лежащая напротив угла в \(\displaystyle 30^{\circ}{ \small ,}\) в два раза короче гипотенузы: \(\displaystyle CK=\frac{CD}{2}=\frac{2\sqrt{2}}{2}=\sqrt{2}\small.\) | 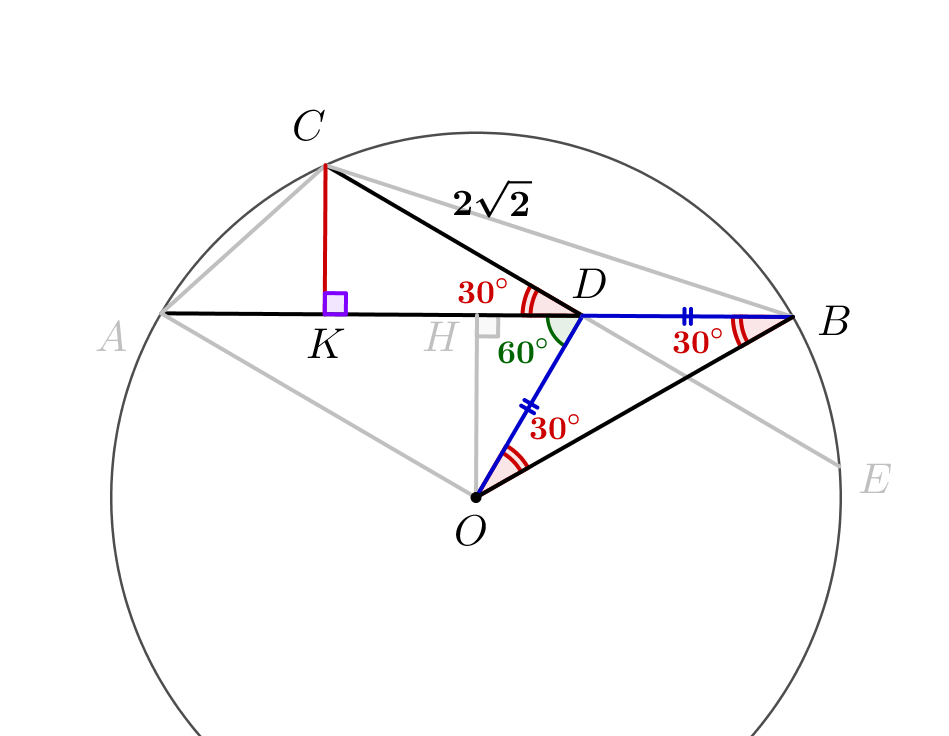 |
Площадь треугольника равна произведению высоты и основания пополам:
\(\displaystyle S_{ABC}=\frac{CK\cdot AB}{2}=\frac{\sqrt{2}\cdot6}{2}=3\sqrt{2}\small.\)
Ответ: \(\displaystyle S_{ABC}=3\sqrt{2}\small.\)