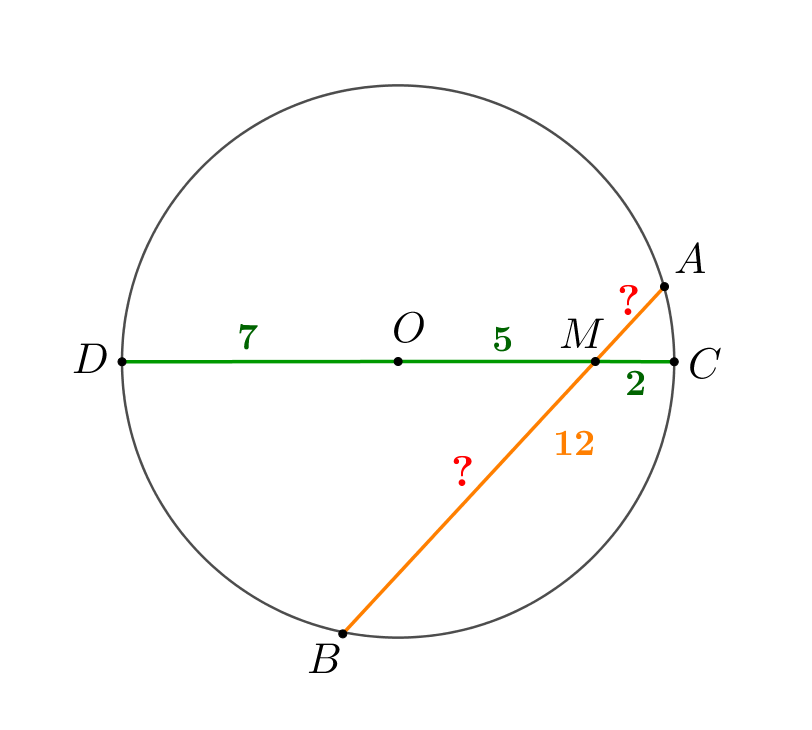
Точка \(\displaystyle M\) удалена на расстояние, равное \(\displaystyle 5,\) от центра окружности, радиус которой равен \(\displaystyle R=7\small.\) Через \(\displaystyle M\) провели хорду, равную \(\displaystyle 12\small.\) Найдите отрезки, на которые делится хорда точкой \(\displaystyle M\small.\)
Точка \(\displaystyle O\) – центр окружности. Хорда \(\displaystyle AB\) проходит через \(\displaystyle M\) и имеет длину \(\displaystyle 12\small.\) Диаметр \(\displaystyle CD\) проходит через \(\displaystyle M\small.\) Найдем длину отрезков, на которые \(\displaystyle M\) делит \(\displaystyle CD{\small:}\)
|  |
Воспользуемся правилом:
Теорема об отрезках пересекающихся хорд
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды:
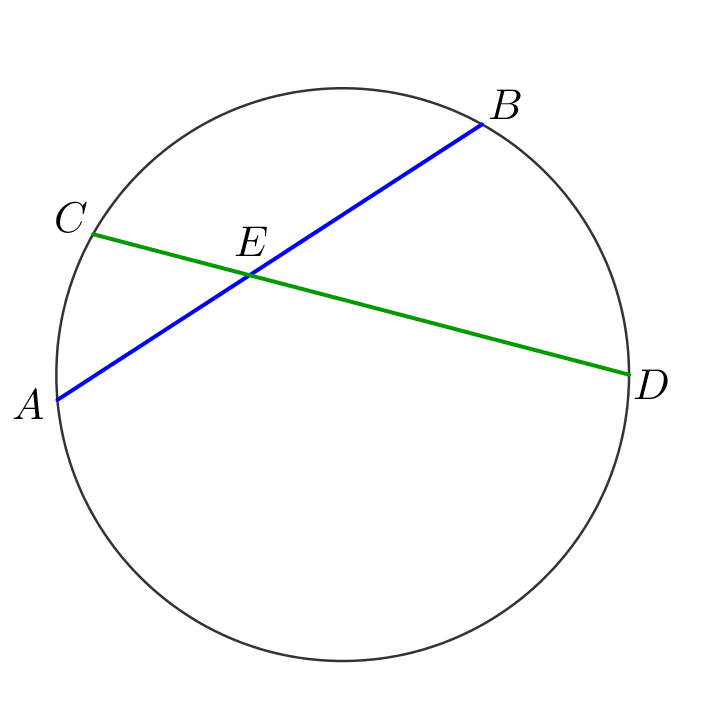
\(\displaystyle \color{blue}{AE}\cdot \color{blue}{BE}=\color{green}{CE}\cdot \color{green}{ DE}\)
Тогда
\(\displaystyle AM\cdot BM=CM\cdot DM=2\cdot12=24\small.\)
То есть мы знаем сумму и произведение длин \(\displaystyle AM\) и \(\displaystyle BM{\small:}\)
\(\displaystyle AM\cdot BM=24\) и \(\displaystyle AM+BM=AB=12\small.\)
Тогда по теореме Виета \(\displaystyle AM\) и \(\displaystyle BM\) – корни уравнения
\(\displaystyle x^2-12x+24=0\small.\)
\(\displaystyle x_1=6+2\sqrt{3}\) и \(\displaystyle x_2=6-2\sqrt{3}\small.\)
То есть точка \(\displaystyle M\) делит \(\displaystyle AB\) на отрезки длины \(\displaystyle 6+2\sqrt{3}\) и \(\displaystyle 6-2\sqrt{3}\small.\)
Ответ: \(\displaystyle 6+2\sqrt{3}\) и \(\displaystyle 6-2\sqrt{3}\small.\)