Точка \(\displaystyle P\) лежит вне окружности радиуса \(\displaystyle 6\) с центром \(\displaystyle O\small.\) Через \(\displaystyle P\) провели секущую, пересекающую окружность в точках \(\displaystyle A\) и \(\displaystyle B\small.\) Найдите \(\displaystyle PA\small,\) если \(\displaystyle PB=5\) и \(\displaystyle OP=10\small.\)
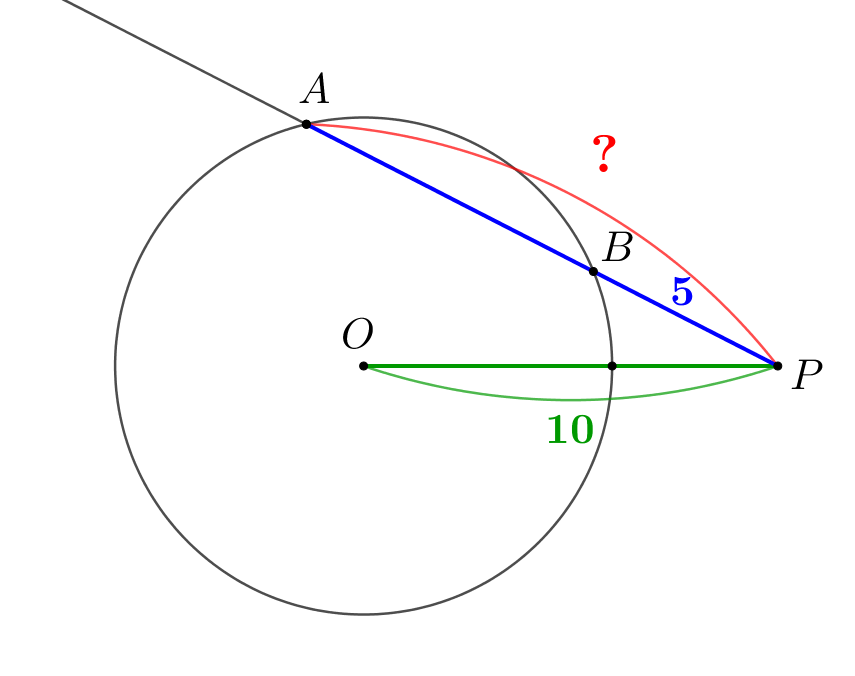
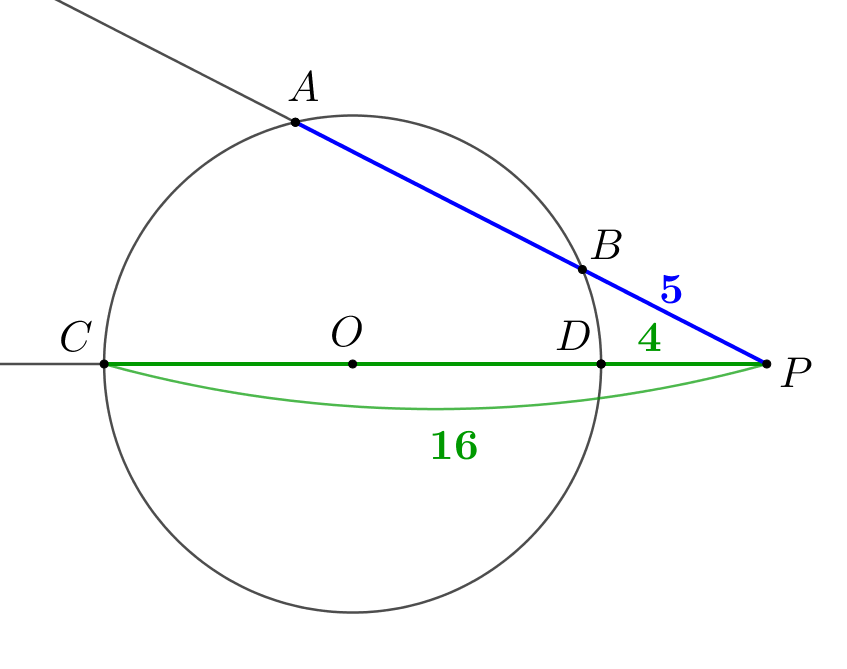
Проведем секущую через точки \(\displaystyle P\) и \(\displaystyle O\small.\) Пусть она пересекает окружность в точках \(\displaystyle C\) и \(\displaystyle D\small.\) Поскольку радиус окружности равен \(\displaystyle 6\small,\) то
|  |
Сумма противоположных углов вписанного четырехугольника равна \(\displaystyle 180^{\circ}{\small:}\) \(\displaystyle \angle ACD=180^{\circ}-\angle DBA\small.\) Значит, \(\displaystyle \angle DBP=180^{\circ}-\angle DBA=\angle ACD\small.\)
Тогда треугольники \(\displaystyle APC\) и \(\displaystyle DPB\) подобны по двум углам. Значит, выполняется равенство: \(\displaystyle \frac{AP}{DP}=\frac{CP}{BP}\small.\) | 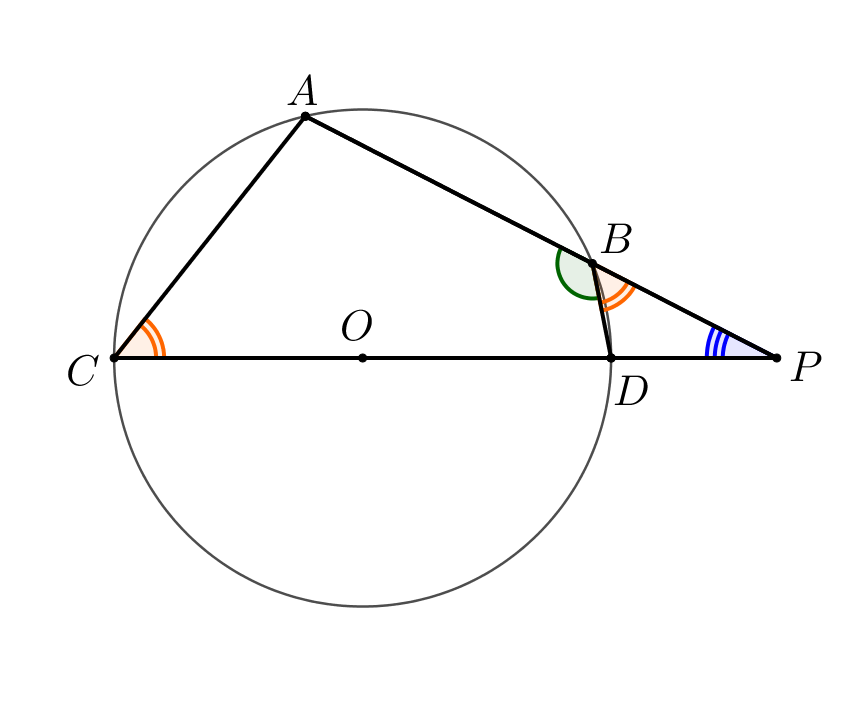 |
Подставляя известные значения \(\displaystyle BP=5,\,CP=16,\,DP=4\small,\) получаем:
\(\displaystyle \frac{AP}{4}=\frac{16}{5}\small,\)
\(\displaystyle AP=\frac{4\cdot16}{5}=12{,}8\small.\)
Ответ: \(\displaystyle AP=12{,}8\small.\)
Отметим, что в процессе решения мы получили:
\(\displaystyle \frac{AP}{DP}=\frac{CP}{BP}\small.\)
Значит, справедливо правило:
Теорема об отрезках секущих
Если две секущие проходят через одну точку, то произведение отрезков одной секущей равно произведению отрезков другой секущей:
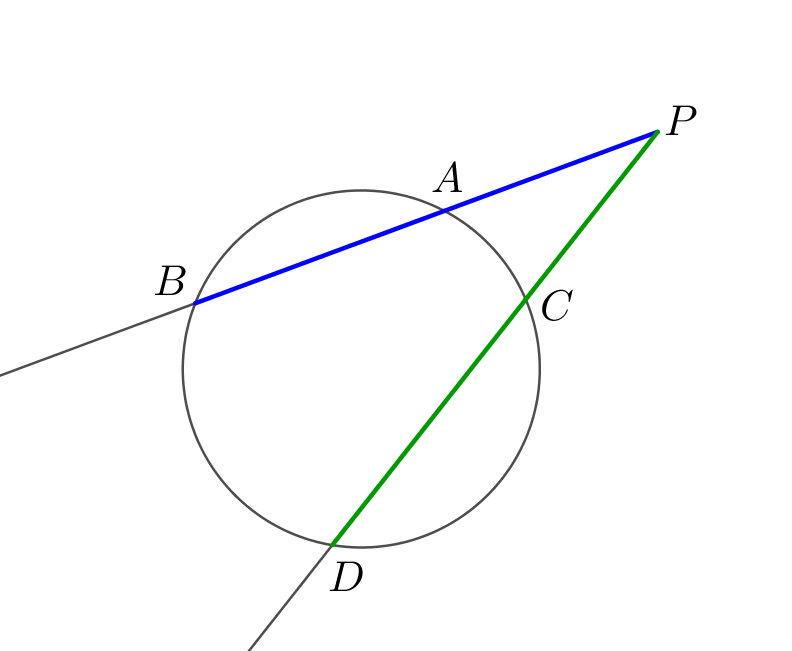
\(\displaystyle \color{blue}{AP}\cdot \color{blue}{BP}=\color{green}{CP}\cdot \color{green}{ DP}\)