Задание
Расставьте отрезки так, чтобы получилось верное равенство.
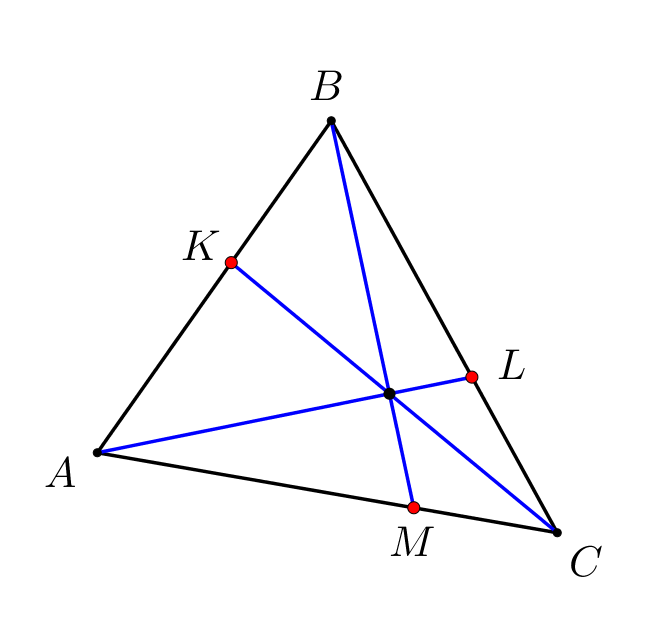
Отрезки \(\displaystyle AL,\,BM\) и \(\displaystyle CK\) пересекаются в одной точке. Тогда
Замечание / комментарий
Данное утверждение называется теоремой Чевы.
Решение
Чтобы верно записать теорему Чевы, необходимо, двигаясь по кругу, последовательно запиcывать отрезки в числитель и знаменатель.
Записываем:
Получаем: \(\displaystyle \frac{\color{blue}{AK}}{\color{red}{KB}}\cdot\frac{\color{blue}{BL}}{\color{red}{LC}}\cdot\frac{\color{blue}{CM}}{\color{red}{MA}}=1\small.\) | 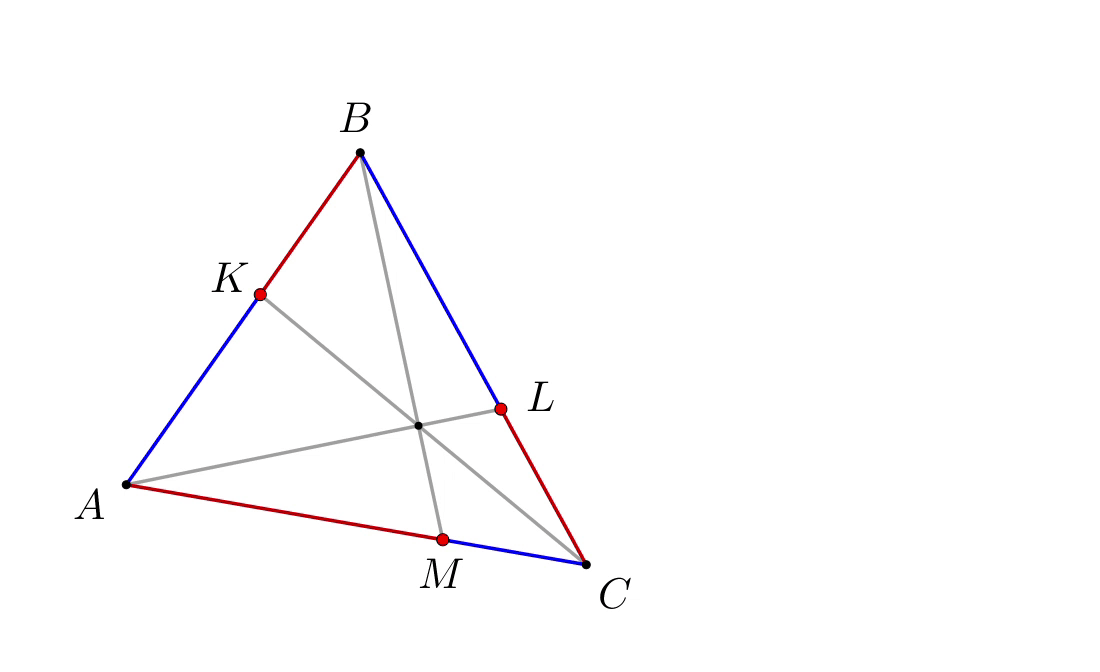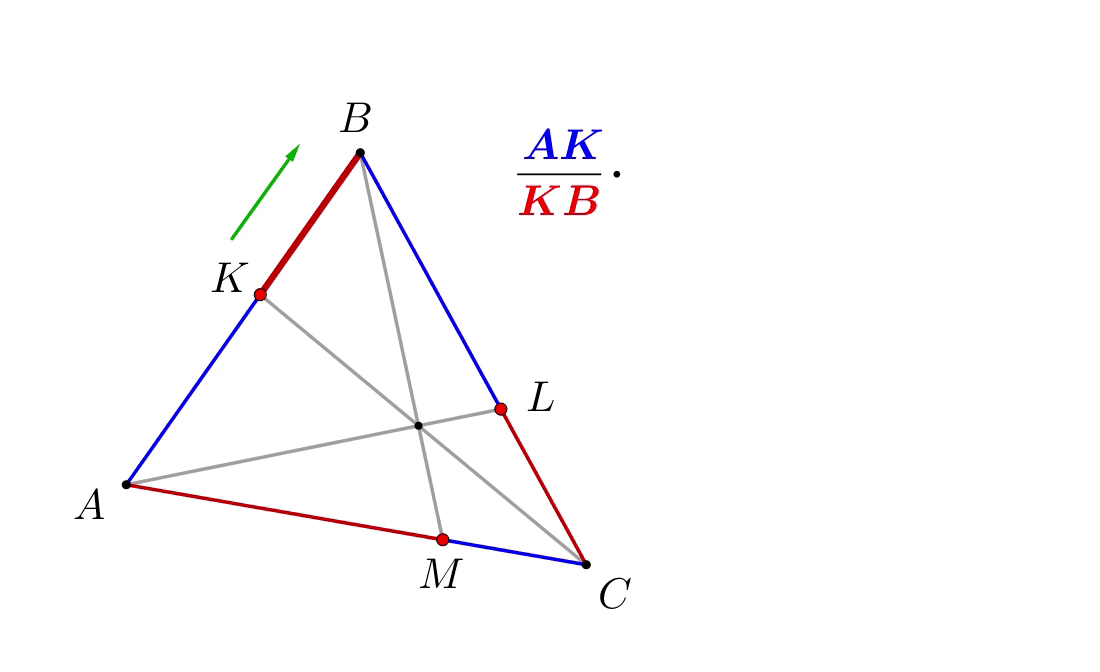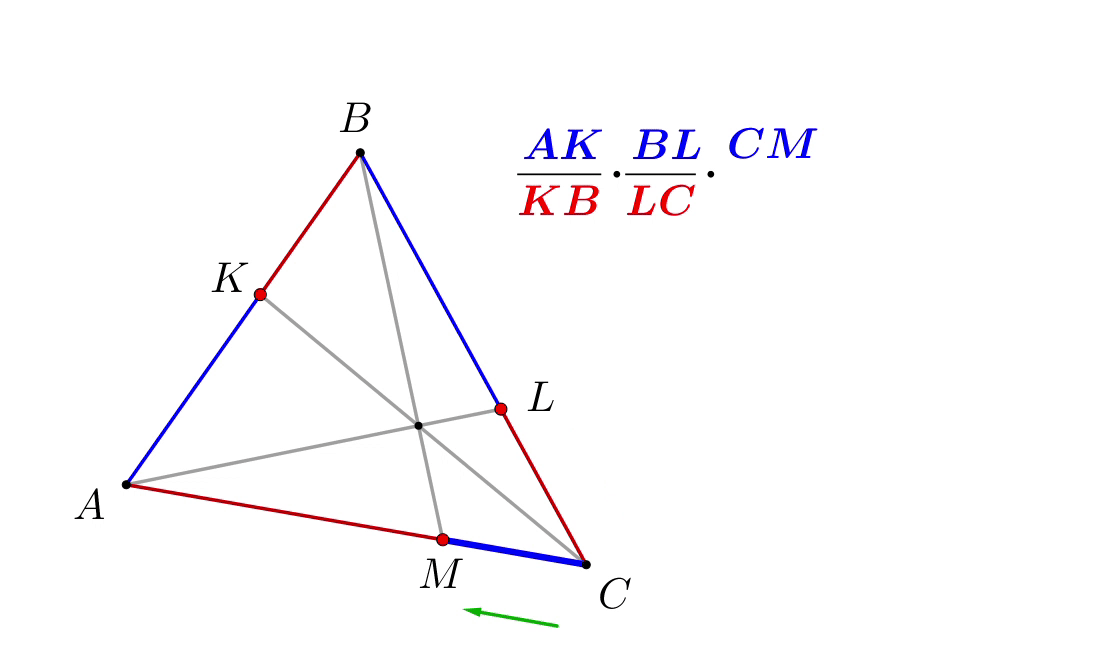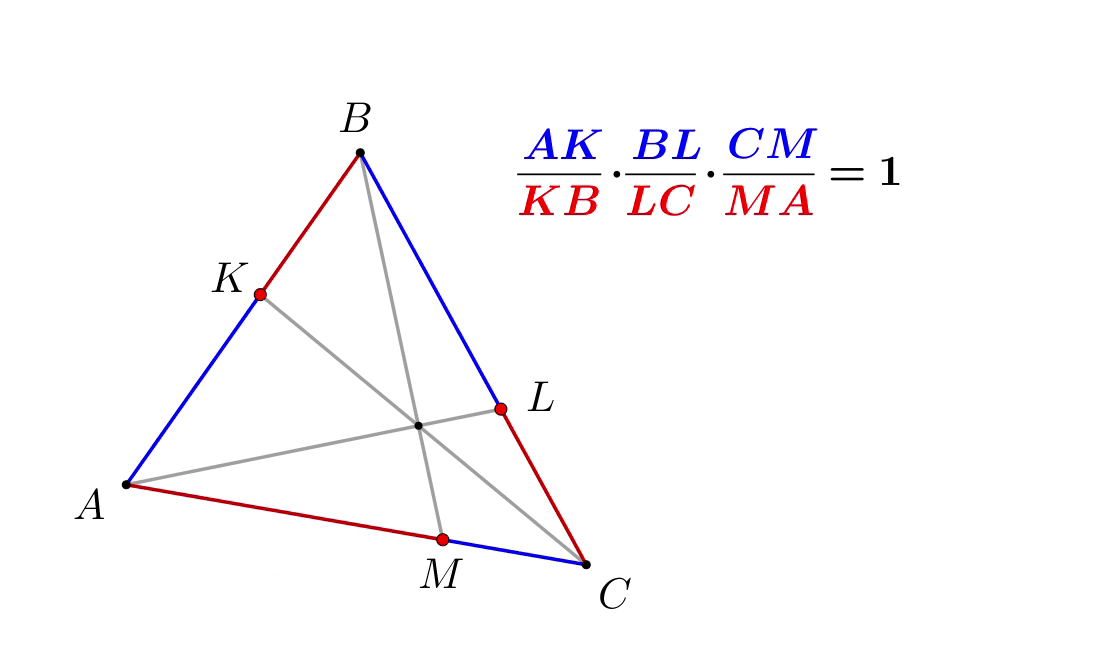 |