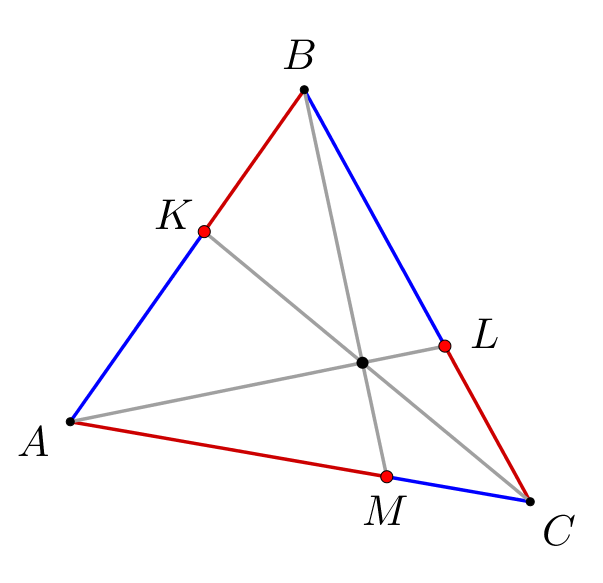
Медиана \(\displaystyle BM\) треугольника \(\displaystyle ABC\) пересекается с чевианой \(\displaystyle AK\) в точке \(\displaystyle P\small.\) Найдите длину отрезков, на которые прямая \(\displaystyle CX\) делит сторону \(\displaystyle AB\small,\) если \(\displaystyle BK:CK=1:2\) и \(\displaystyle AB=18\small.\)
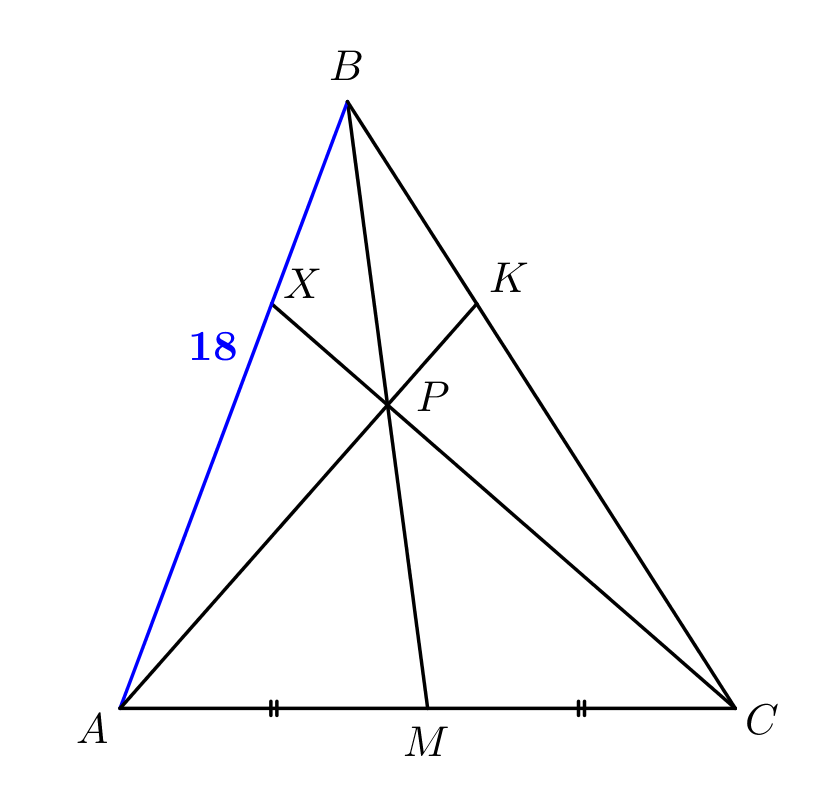
(Чевианой треугольника называется отрезок, соединяющий вершину треугольника с точкой на противоположной стороне. )
Отрезки \(\displaystyle AK,\,BM\) и \(\displaystyle CX\) пересекаются в одной точке. Тогда по теореме Чевы для треугольника \(\displaystyle ABC\) получаем: \(\displaystyle \frac{\color{blue}{AX}}{\color{red}{XB}}\cdot\frac{\color{blue}{BK}}{\color{red}{KC}}\cdot\frac{\color{blue}{CM}}{\color{red}{MA}}=1\small.\) | 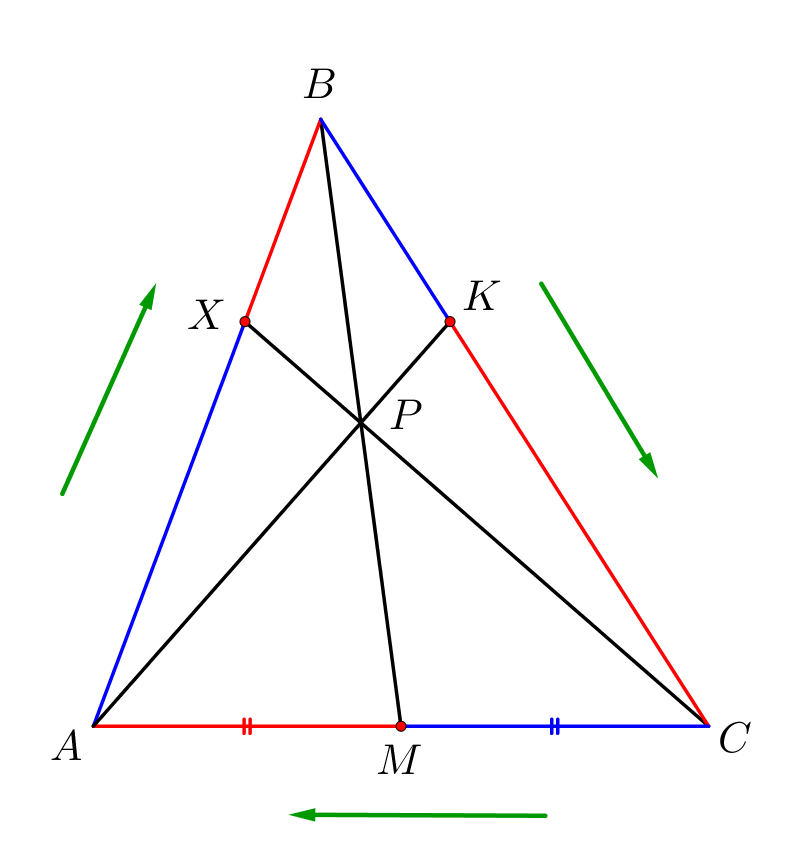 |
Подставим известные отношения \(\displaystyle BK:CK=1:2\) и \(\displaystyle CM:AM=1{\small:}\)
\(\displaystyle \frac{AX}{BX}\cdot\frac{1}{2}\cdot1=1\small.\)
Тогда
\(\displaystyle AX=2BX\small.\)
Также из условия известно, что
\(\displaystyle 18=AB=AX+BX\small.\)
Подставим \(\displaystyle AX=2BX\) и найдем длины отрезков \(\displaystyle AX\) и \(\displaystyle BX{\small:}\)
\(\displaystyle 2BX+BX=18\small,\)
\(\displaystyle BX=18:3=6\) и \(\displaystyle AX=2BX=12\small.\)
Ответ: \(\displaystyle 6\) и \(\displaystyle 12\small.\)