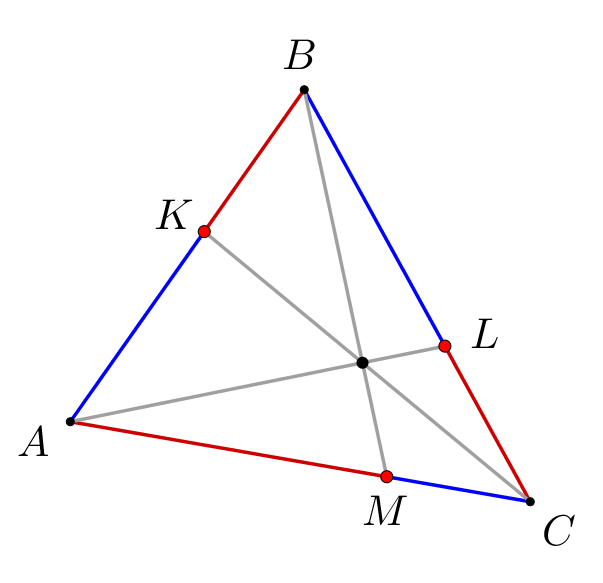
В четырехугольнике \(\displaystyle ABCD\) углы \(\displaystyle B\) и \(\displaystyle C\) равны. Через точку пересечения диагоналей \(\displaystyle O\) провели прямую, параллельную \(\displaystyle AD\small,\) она пересекает \(\displaystyle AB\) и \(\displaystyle CD\) в точках \(\displaystyle M\) и \(\displaystyle K\) соответственно. Найдите \(\displaystyle AB\small,\) если \(\displaystyle CD=6,\,MO=2,\,KO=3\small.\)
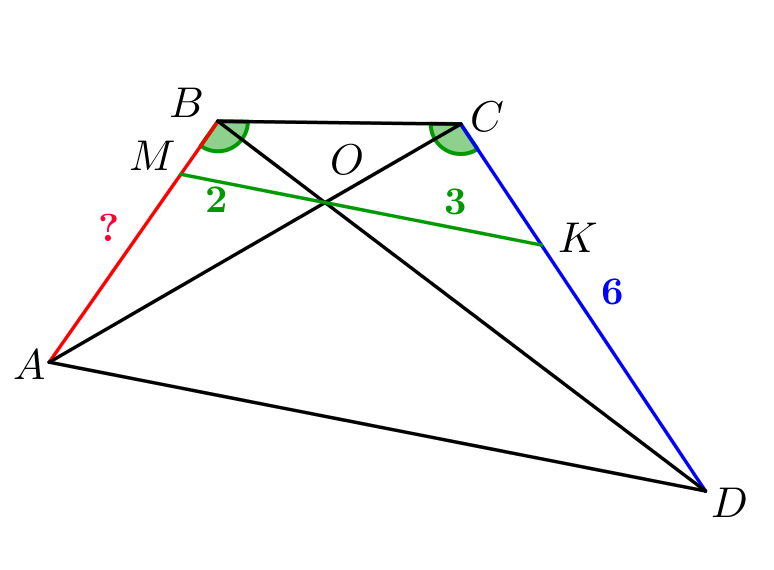
Чтобы воспользоваться теоремой Чевы, продлим стороны \(\displaystyle AB\) и \(\displaystyle CD\) до точки пересечения \(\displaystyle X\small.\) Проведем отрезок \(\displaystyle XN\small,\) проходящий через \(\displaystyle O\small.\)
Тогда по теореме Чевы \(\displaystyle \frac{\color{blue}{AB}}{\color{red}{BX}}\cdot\frac{\color{blue}{XC}}{\color{red}{CD}}\cdot\frac{\color{blue}{DN}}{\color{red}{NA}}=1\small.\) | 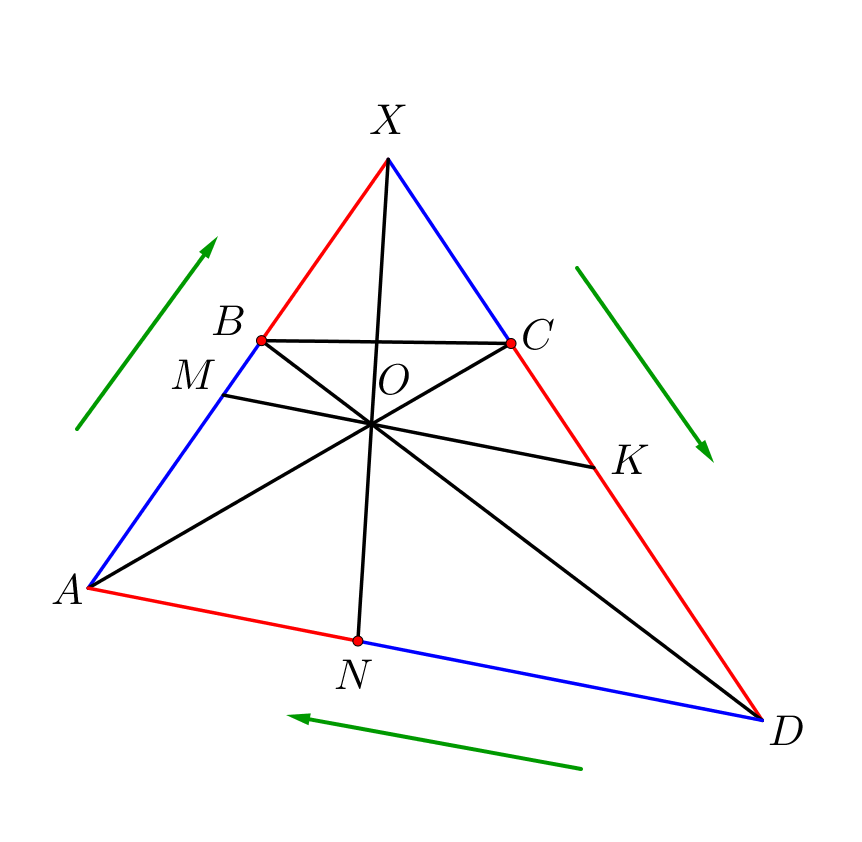 |
\(\displaystyle BX=CX\small.\)
Поскольку углы \(\displaystyle ABC\) и \(\displaystyle DCB\) равны, то и смежные им углы равны: \(\displaystyle \angle XBC=180^{\circ}-\angle ABC=\angle XCB\small.\) Тогда треугольник \(\displaystyle BXC\) равнобедренный и \(\displaystyle \color{orange}{BX}=\color{orange}{CX}\small.\) | 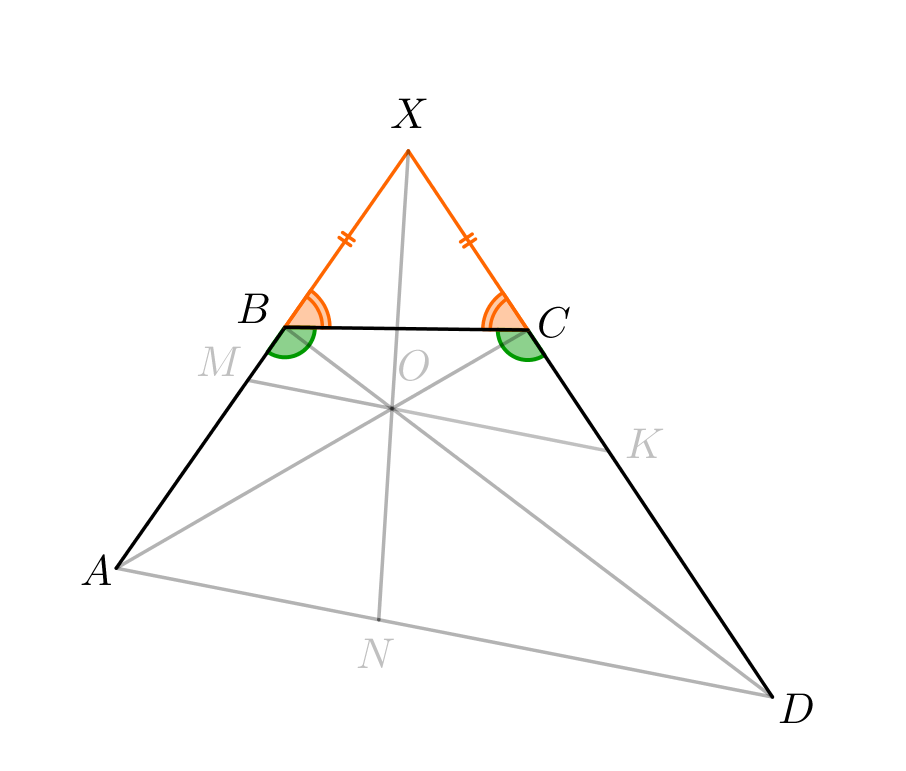 |
Значит,
\(\displaystyle \frac{AB}{\cancel{\color{orange}{BX}}}\cdot\frac{\cancel{\color{orange}{XC}}}{CD}\cdot\frac{DN}{NA}=\frac{AB\cdot DN}{DC\cdot AN}=1\small.\)
Длина отрезка \(\displaystyle CD\) известна, а длину \(\displaystyle AB\) нужно найти.
\(\displaystyle \frac{DN}{AN}=\frac{KO}{MO}=\frac{3}{2}\small.\)
Поскольку прямые \(\displaystyle MK\) и \(\displaystyle AD\) параллельны, то соответственные углы равны: \(\displaystyle \angle XAN=\angle XMO\) и \(\displaystyle \angle XDN=\angle XKO\small.\) Тогда есть две пары подобных треугольников \(\displaystyle AXN,\,MXO\) и \(\displaystyle DXN,\,KXO\small.\) Причем коэффициент подобия одинаковый: \(\displaystyle k=\frac{XN}{XO}\small.\) | 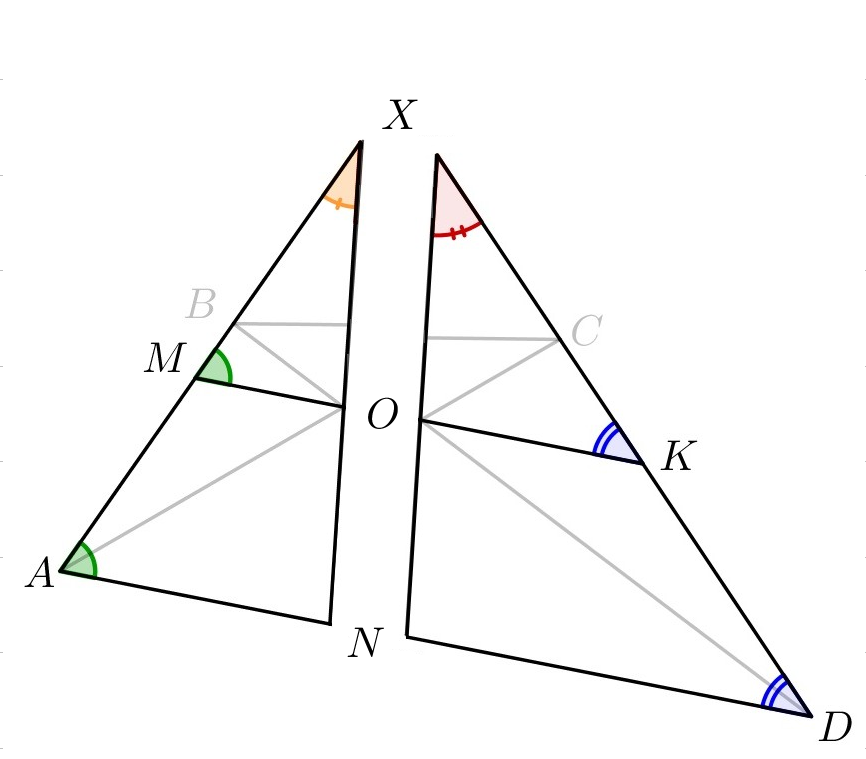 |
Тогда
\(\displaystyle \frac{AN}{MO}=k=\frac{DN}{KO}\small.\)
Используя свойство пропорции и подставляя известные значения \(\displaystyle MO=2,\,KO=3\small,\) получаем:
\(\displaystyle \frac{DN}{AN}=\frac{KO}{MO}=\frac{3}{2}\small.\)
Получаем:
\(\displaystyle \frac{AB\cdot DN}{DC\cdot AN}=\frac{AB}{DC}\cdot\frac{3}{2}=1\small.\)
Подставляя \(\displaystyle CD=6\small,\) находим \(\displaystyle AB{\small:}\)
\(\displaystyle AB=\frac{2\cdot6}{3}=4\small.\)
Ответ: \(\displaystyle AB=4\small.\)