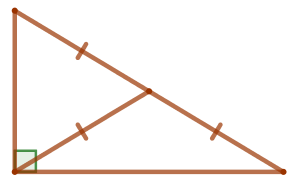
Диагональ прямоугольной трапеции и её боковая сторона равны и перпендикулярны. Найдите высоту трапеции, если бóльшее основание трапеции равно \(\displaystyle 20{\small.}\)
Пусть \(\displaystyle ABCD\) – прямоугольная трапеция:
Требуется найти высоту данной трапеции. | 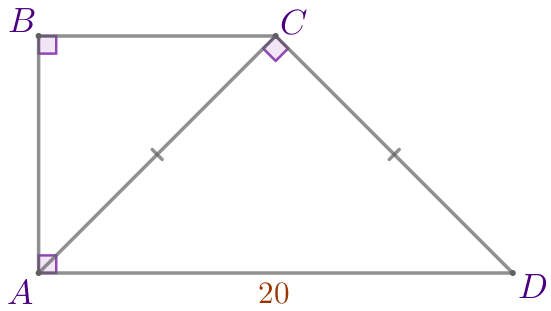 |
Из вершины \(\displaystyle C\) проведём высоту \(\displaystyle CH{\small.}\)
Рассмотрим треугольник \(\displaystyle ACD{\small:}\)
Значит, \(\displaystyle \triangle ACD\) – прямоугольный и равнобедренный. | 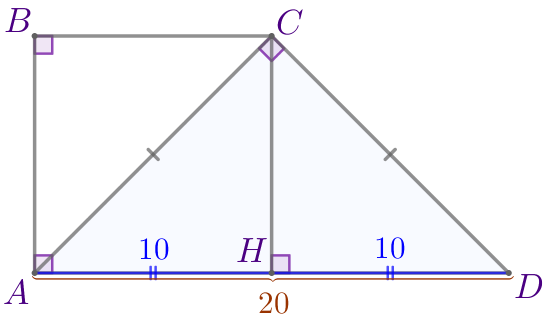 |
В равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.
\(\displaystyle CH\) – медиана прямоугольного треугольника, проведённая к гипотенузе.
Следовательно,
\(\displaystyle CH=\frac{1}{2} \cdot AD=\frac{1}{2} \cdot 20=10{\small.}\)
Высота трапеции равна \(\displaystyle 10{\small.}\)
Ответ: \(\displaystyle 10{\small.}\)