Из вершины прямого угла меньшего основания прямоугольной трапеции под углом \(\displaystyle 45^{\circ}\) к этому основанию проведён луч, который проходит через середину большей боковой стороны. Найдите меньшую боковую сторону этой трапеции, если её основания равны \(\displaystyle 2\) и \(\displaystyle 3{\small.}\)
По условию задачи выполним построение.
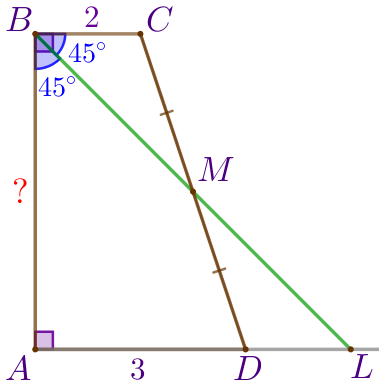
Пусть \(\displaystyle ABCD\) – прямоугольная трапеция:
| 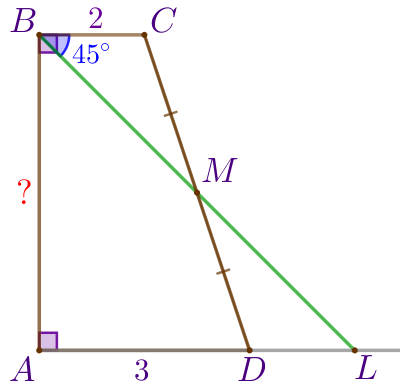 |
Требуется найти меньшую боковую cторону данной трапеции, то есть найти \(\displaystyle AB{\small.}\)
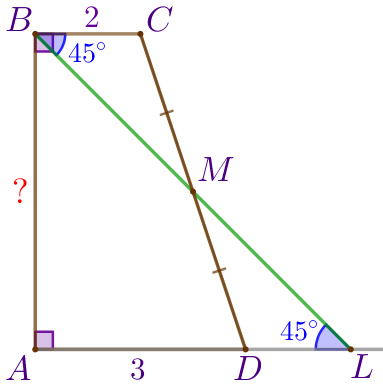
\(\displaystyle \angle ABL=45^{\circ}{\small,}\)
\(\displaystyle \angle ALB=45^{\circ}{\small.}\)
|
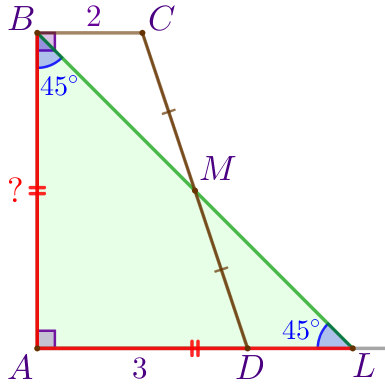
Следовательно, \(\displaystyle \triangle ABL\) – равнобедренный прямоугольный треугольник. Значит, \(\displaystyle \color{red}{AB}=\color{red}{AL}{\small.}\) |
Так как точка \(\displaystyle L\) лежит на продолжении основания \(\displaystyle AD{\small,}\) то
\(\displaystyle \color{red}{AL}=AD+DL=3+DL{\small.}\)
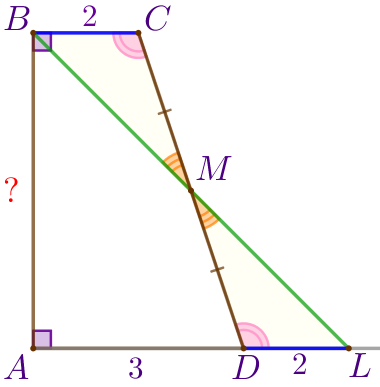
Рассмотрим треугольники \(\displaystyle CMB\) и \(\displaystyle DML{\small.}\)
|
Следовательно, \(\displaystyle \triangle CMB= \triangle DML\) по стороне и двум прилежащим углам. |
Значит,
\(\displaystyle DL=BC=2{\small.}\)
Тогда
\(\displaystyle \color{red}{AL}=3+DL=3+2=5{\small.}\)
Получили:
\(\displaystyle \color{red}{AB}=\color{red}{AL}=5{\small.}\)
Меньшая боковая сторона трапеции равна \(\displaystyle 5{\small.}\)
Ответ: \(\displaystyle 5{\small.}\)