В прямоугольной трапеции \(\displaystyle ABCD\) \(\displaystyle (AD\parallel BC{\small,}\, \, AB \perp AD)\) диагональ \(\displaystyle AC\) перпендикулярна боковой стороне \(\displaystyle CD{\small,}\) \(\displaystyle \angle D=30^{\circ}{\small.}\) Найдите меньшее основание трапеции, если бóльшее основание равно \(\displaystyle 24\, \footnotesize см{\small.}\)
\(\displaystyle \footnotesize см{\small.}\)
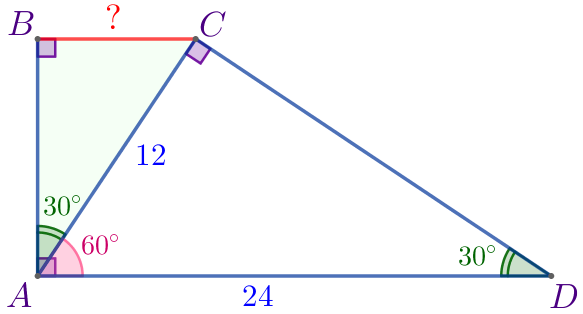
Пусть \(\displaystyle ABCD\) – прямоугольная трапеция:
| 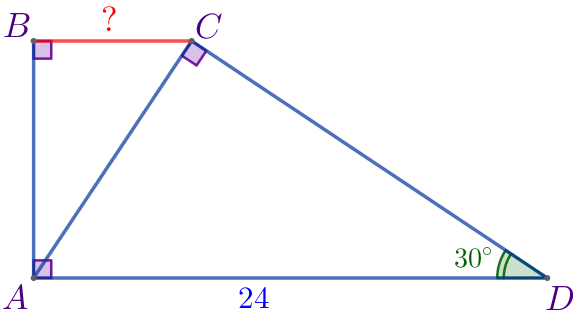 |
Требуется найти меньшее основание данной трапеции, то есть найти основание \(\displaystyle BC{\small.}\)
\(\displaystyle \triangle ADC\) – прямоугольный, \(\displaystyle \angle ADC=30^{\circ}{\small.}\) Сумма острых углов прямоугольного треугольника равна \(\displaystyle 90^{\circ}{\small.}\) Значит, \(\displaystyle \angle CAD=90^{\circ}-\angle ADC{\small;}\) \(\displaystyle \angle CAD=90^{\circ}-30^{\circ}=60^{\circ}{\small.}\) | 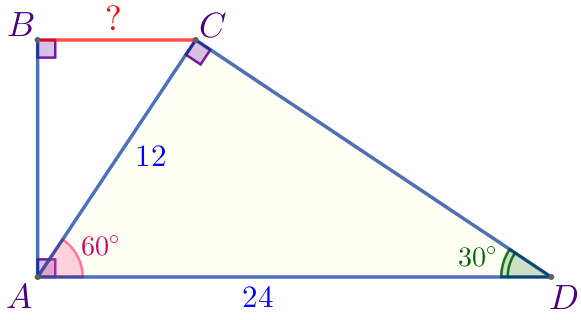 |
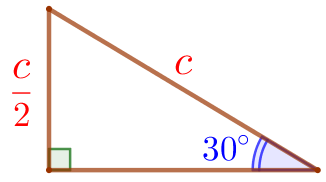
| Катет прямоугольного треугольника, лежащий против угла в \(\displaystyle 30^{\circ}{\small,}\) равен половине гипотенузы |
|
Следовательно,
\(\displaystyle AC=\frac{1}{2} \cdot AD=\frac{1}{2} \cdot 24=12{\small.}\)
| \(\displaystyle \triangle ABC\) – прямоугольный.
\(\displaystyle \angle BAC=\angle BAD- \angle CAD{\small;}\) \(\displaystyle \angle BAC=90^{\circ}- 60^{\circ}=30^{\circ}{\small.}\) |
Катет \(\displaystyle BC\) лежит против угла в \(\displaystyle 30^{\circ}{\small.}\) Следовательно,
\(\displaystyle BC=\frac{1}{2} \cdot AC=\frac{1}{2} \cdot 12=6{\small.}\)
Меньшее основание трапеции равно \(\displaystyle 6{\small.}\)
Ответ: \(\displaystyle 6{\small.}\)