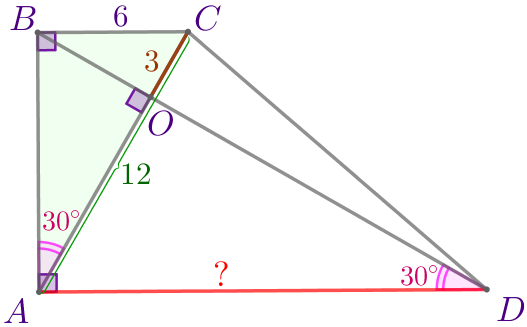
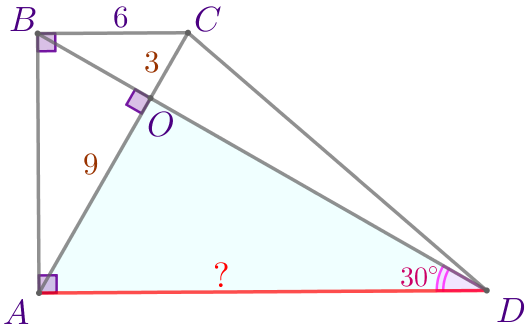
В прямоугольной трапеции диагонали взаимно перпендикулярны. Большая диагональ составляет с меньшей боковой стороной угол в \(\displaystyle 60^{\circ}{\small.}\) Найдите бóльшее основание трапеции, если меньшее основание этой трапеции равно \(\displaystyle 6{\small.}\)
По условию задачи выполним построение.
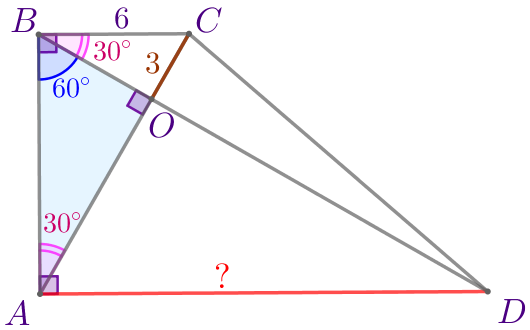
Пусть \(\displaystyle ABCD\) – прямоугольная трапеция:
| 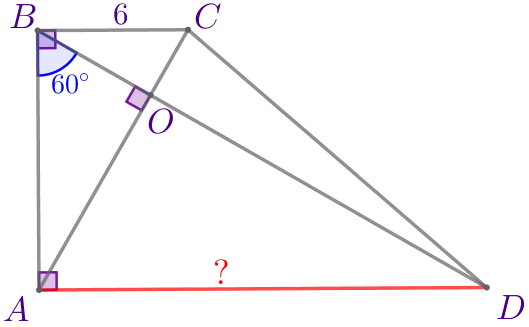 |
Требуется найти бóльшее основание данной трапеции, то есть найти основание \(\displaystyle AD{\small.}\)
\(\displaystyle \angle BOC=90^{\circ}{\Rightarrow}\)\(\displaystyle \triangle BOC\) – прямоугольный.
\(\displaystyle \angle CBO=\angle ABC- \angle ABO{\small;}\) \(\displaystyle \angle CBO=90^{\circ}- 60^{\circ}=30^{\circ}{\small.}\) | 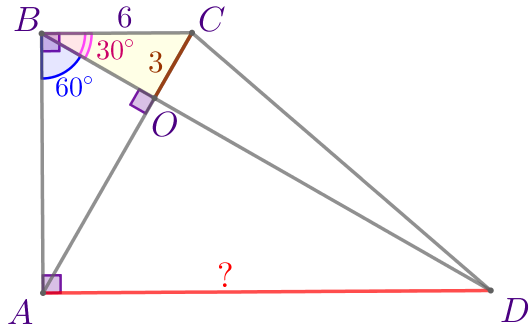 |
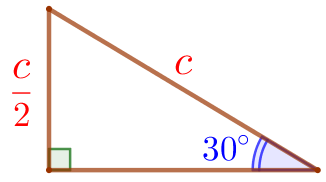
| Катет прямоугольного треугольника, лежащий против угла в \(\displaystyle 30^{\circ}{\small,}\) равен половине гипотенузы |
|
Следовательно,
\(\displaystyle OC=\frac{1}{2} \cdot BC=\frac{1}{2} \cdot 6=3{\small.}\)
\(\displaystyle \angle BAC=30^{\circ}{\small,}\)
\(\displaystyle \angle ADO=30^{\circ}{\small.}\)
| \(\displaystyle \triangle ABC\) – прямоугольный, \(\displaystyle \angle BAC=30^{\circ}{\small.}\) Катет \(\displaystyle BC\) лежит против угла в \(\displaystyle 30^{\circ}{\small.}\) Следовательно, \(\displaystyle BC=\frac{1}{2} \cdot AC{\small.}\) Значит, \(\displaystyle AC=2BC=2 \cdot 6=12{\small.}\) |
Точка \(\displaystyle O\) лежит на диагонали \(\displaystyle AC{\small,}\) тогда
\(\displaystyle AO=AC-OC=12-3=9{\small.}\)
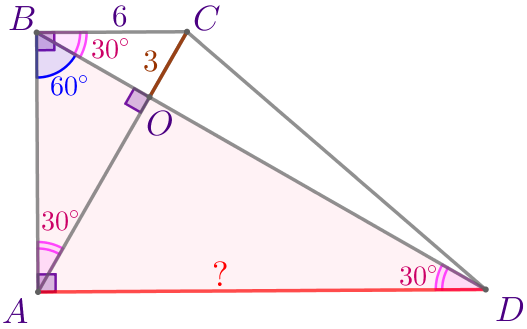
| \(\displaystyle \triangle AOD\) – прямоугольный, \(\displaystyle \angle ADO=30^{\circ}{\small.}\) Катет \(\displaystyle AO\) лежит против угла в \(\displaystyle 30^{\circ}{\small.}\) Следовательно, \(\displaystyle AO=\frac{1}{2} \cdot AD{\small.}\) Значит, \(\displaystyle AD=2AO=2 \cdot 9=18{\small.}\) |
Бóльшее основание трапеции равно \(\displaystyle 18{\small.}\)
Ответ: \(\displaystyle 18{\small.}\)