В треугольнике \(\displaystyle ABC\) точки \(\displaystyle M\) и \(\displaystyle N\) являются серединами сторон \(\displaystyle AB\) и \(\displaystyle BC\) соответственно. Найдите сторону \(\displaystyle AC{\small,}\) если \(\displaystyle MN=7{\small.}\)
\(\displaystyle AC=\)
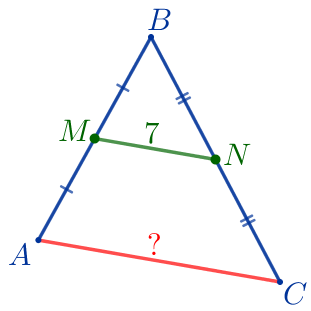 | Треугольник \(\displaystyle ABC{\small:}\)
Требуется найти сторону \(\displaystyle AC{\small.}\) |
Средняя линия треугольника параллельна его основанию и равна половине основания. |  |
Согласно свойству
\(\displaystyle MN=\frac{1}{2} \cdot AC{\small.}\)
Тогда
\(\displaystyle AC=2 \cdot MN=2 \cdot 7=14{\small.}\)
Ответ: \(\displaystyle AC=14{\small.}\)
