Отрезок, соединяющий середины сторон \(\displaystyle AB\) и \(\displaystyle AC\) треугольника \(\displaystyle ABC{\small,}\) на \(\displaystyle 3\, \footnotesize см\) меньше стороны \(\displaystyle BC{\small,}\) на \(\displaystyle 4\, \footnotesize см\) меньше стороны \(\displaystyle AB\) и на \(\displaystyle 5\, \footnotesize см\) меньше стороны \(\displaystyle AC{\small.}\) Найдите периметр треугольника \(\displaystyle ABC{\small.}\)
\(\displaystyle P_{\triangle ABC}=\) \(\displaystyle \footnotesize см{\small.}\)
\(\displaystyle ABC\) – треугольник:
Пусть \(\displaystyle MN=x{\small,}\) тогда по условию задачи
Требуется найти периметр треугольника \(\displaystyle ABC{\small.}\) | 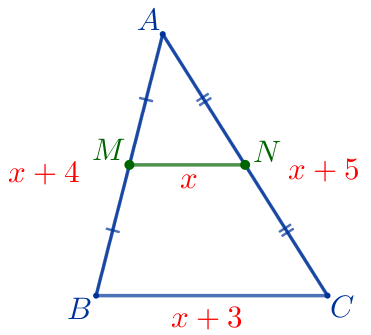 |
Периметр треугольника равен сумме длин всех его сторон:
\(\displaystyle P_{\triangle ABC}=AB+BC+AC=\color{red}{\large ?}\)
\(\displaystyle P_{\triangle ABC}=x+4+x+3+x+5=3x+12=\color{red}{\large ?}\)
\(\displaystyle MN=\frac{1}{2} \cdot BC\, \, \, \Longrightarrow\, \, \, BC=2 \cdot MN{\small;}\)
Подставим \(\displaystyle BC=x+3{\small,}\) \(\displaystyle MN=x{\small:}\)
\(\displaystyle x+3=2\cdot x{\small;}\)
\(\displaystyle x=3{\small.}\)
Тогда
\(\displaystyle P_{\triangle ABC}=3x+12=3 \cdot 3+12=9+12=21\, \footnotesize см{\small.}\)
Ответ: \(\displaystyle P_{\triangle ABC}=21\, \footnotesize см{\small.}\)

