Найдите среднюю линию равностороннего треугольника, если его периметр равен \(\displaystyle 96{\small.}\)
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Третью сторону треугольника, с которой его средняя линия не имеет общих точек, называют основанием. |  |
Пусть \(\displaystyle ABC\) – равносторонний треугольник:
Требуется найти длину средней линии. | 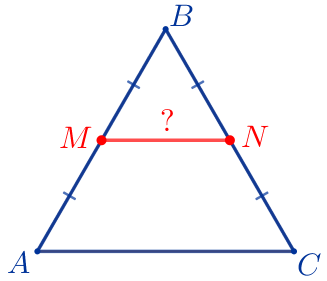 |
Средняя линия треугольника параллельна его основанию и равна половине основания. |  |
Согласно свойству
\(\displaystyle MN=\frac{1}{2} \cdot AC{\small.}\)
Периметр треугольника равен сумме длин всех его сторон:
\(\displaystyle P_{\triangle ABC}=AB+BC+AC{\small.}\)
Так как в равностороннем треугольнике все стороны равны, то
\(\displaystyle P_{\triangle ABC}=3 \cdot AC{\small.}\)
Подставим \(\displaystyle P_{\triangle ABC}=96{\small:}\)
\(\displaystyle 96=3 \cdot AC{\small;}\)
\(\displaystyle AC=32{\small.}\)
В результате получаем:
\(\displaystyle MN=\frac{1}{2} \cdot AC=\frac{1}{2} \cdot 32=16{\small.}\)
Ответ: \(\displaystyle 16{\small.}\)
В равностороннем треугольнике все стороны равны, значит, равны все средние линии.