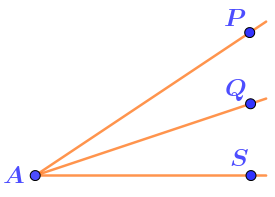
На рисунке три луча \(\displaystyle AP{\small ,\;}AQ\) и \(\displaystyle AS\) с общим началом.
Известны величины углов:
\(\displaystyle \angle PAS=43\degree {\small ,\;}\angle QAS=24\degree{\small .}\)
Найти величину угла \(\displaystyle QAP{\small .}\)
\(\displaystyle \angle QAP=\)\(\displaystyle \degree \)
На рисунке угол \(\displaystyle PAS\) лучом \(\displaystyle AQ\) разбит на два угла – \(\displaystyle QAP\) и \(\displaystyle QAS{\small .}\)
Если угол разбит на части, то величина угла равна сумма величин его частей.

Значит,
\(\displaystyle \angle PAS=\angle QAP+\angle QAS{\small .}\)
Из условия задачи известны сумма и одно из слагаемых.
Найдём неизвестное слагаемое с помощью разности:
\(\displaystyle \angle QAP= \angle PAS-\angle QAS=43\degree -24\degree=19\degree {\small .}\)
Ответ: \(\displaystyle \angle QAP=19\degree{\small .} \)