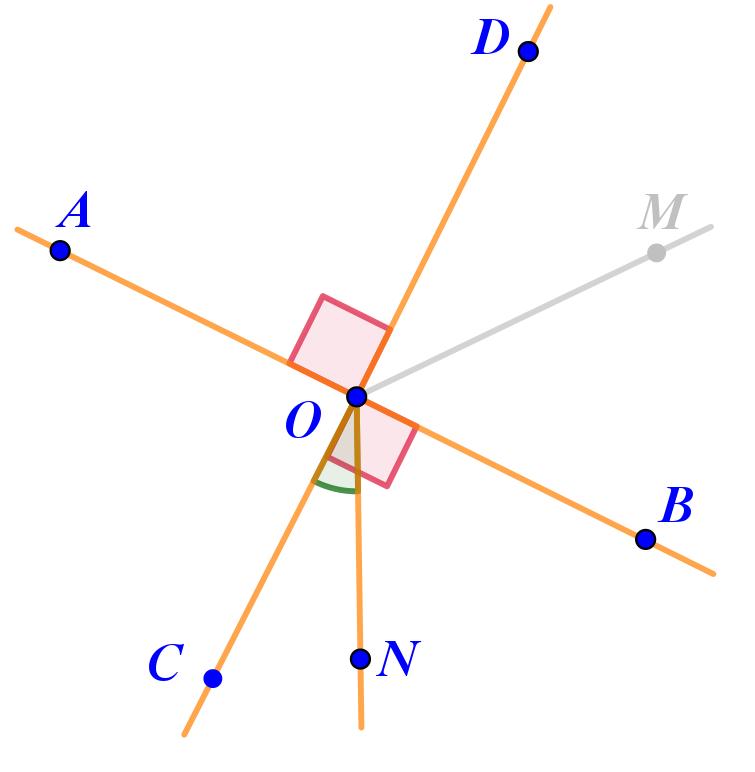
На рисунке отмечен прямой угол, образовавшийся при пересечении двух прямых.
Из точки пересечения прямых выпущены ещё два луча.
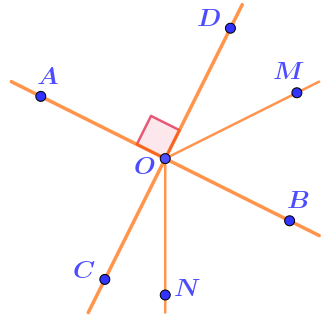
Определите вид нескольких образовавшихся при этом углов.
| \(\displaystyle \angle AOM~-~\) | \(\displaystyle \angle BOM~-~\) | \(\displaystyle \angle CON~-~\) |
| \(\displaystyle \angle AOC~-~\) | \(\displaystyle \angle AON~-~\) | \(\displaystyle \angle COD~-~\) |
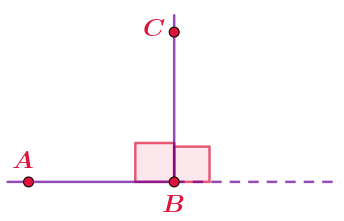
Угол называется острым, если является частью прямого угла.
На рисунке показан угол \(\displaystyle ABC{\small .}\) Он острый, так как является частью прямого угла \(\displaystyle ABD{\small .}\)
Величина острого угла меньше \(\displaystyle 90\degree {\small .}\) | 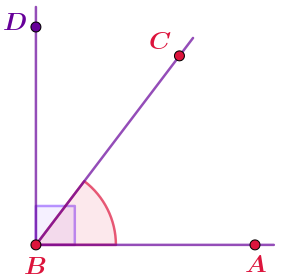 |
| |
Если прямой угол является частью неразвёрнутого угла, то этот угол называется тупым.
На рисунке показан угол \(\displaystyle ABC{\small .}\) Он тупой, так как прямой угол \(\displaystyle ABD\) является его частью.
Величина тупого угла больше \(\displaystyle 90\degree {\small .}\) | 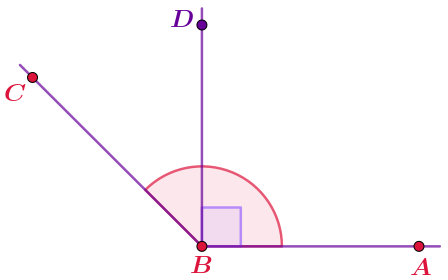 |
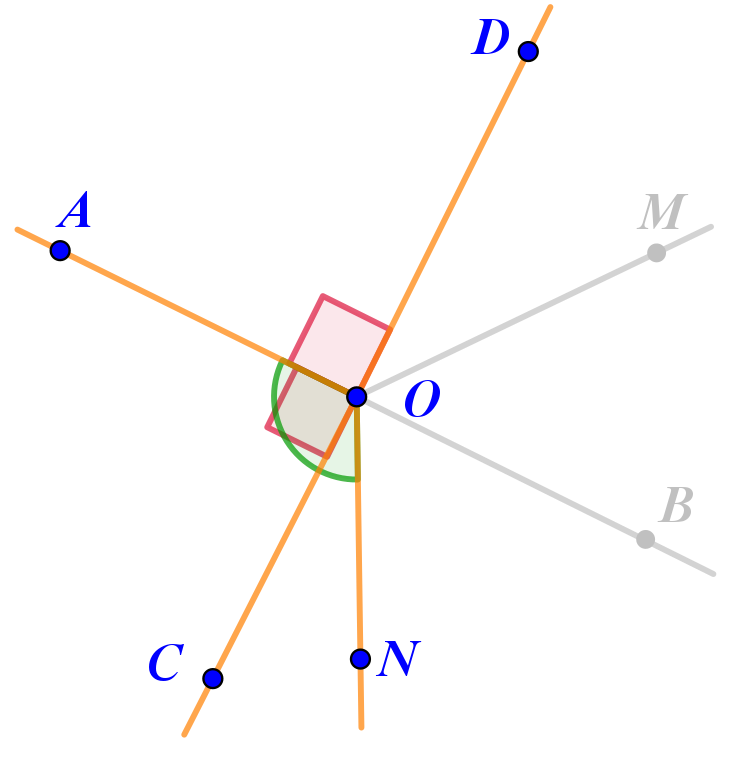
Прямой угол \(\displaystyle AOD\) является частью угла \(\displaystyle AOM{\small .}\)
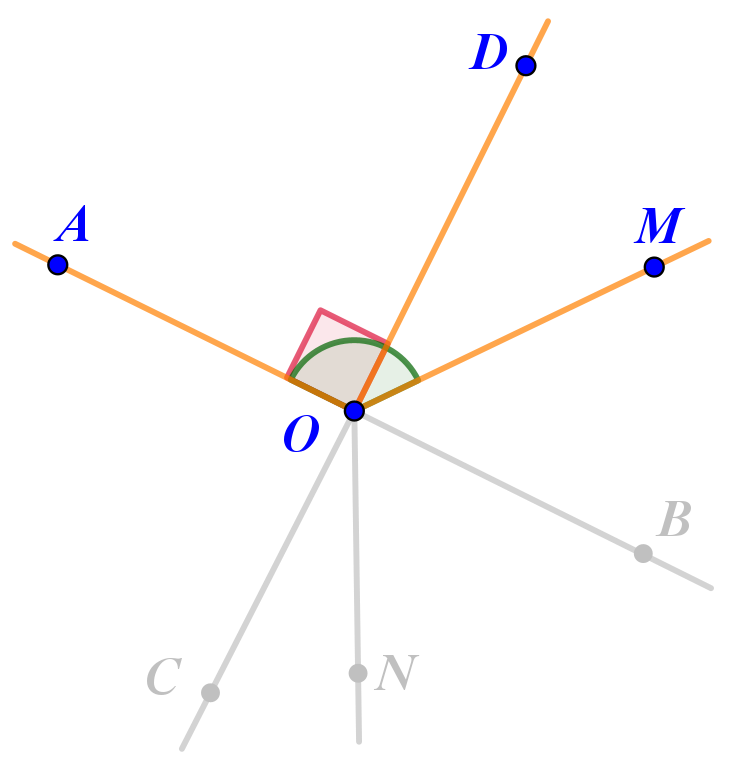
То есть угол \(\displaystyle AOM\) тупой по определению.
Угол \(\displaystyle BOM~-\) часть угла \(\displaystyle BOD{\small ,}\) который является прямым, так как смежен с прямым углом \(\displaystyle AOD{\small .}\)
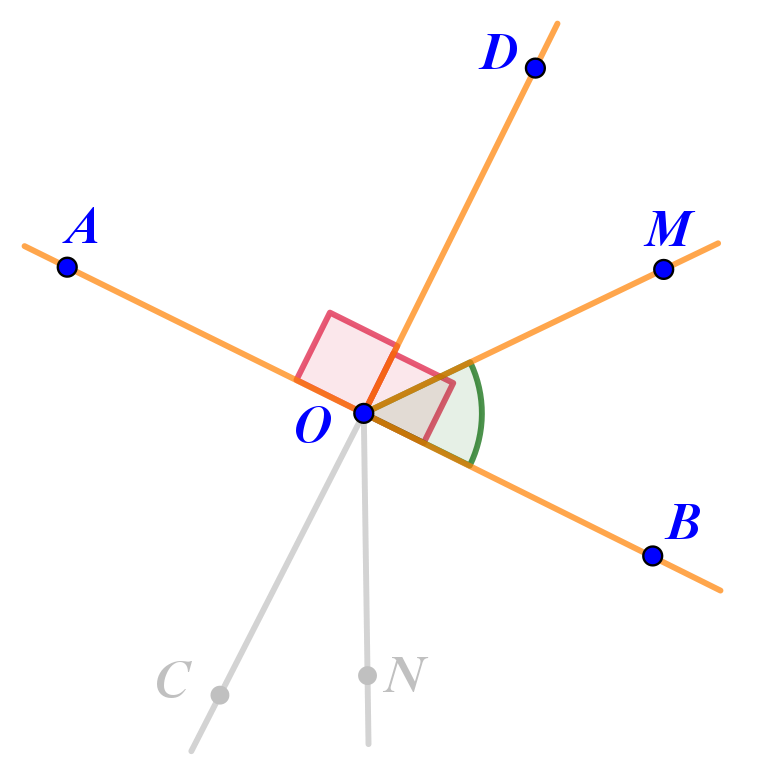
То есть угол \(\displaystyle BOM\) острый по определению.
По условию лучи \(\displaystyle OC\) и \(\displaystyle OD\) дополняют друг друга до прямой.
Значит, угол \(\displaystyle COD\) развёрнутый по определению.
| Ответ: | \(\displaystyle \angle AOM\)– тупой; | \(\displaystyle \angle BOM\)–острый | \(\displaystyle \angle CON\)– острый |
| \(\displaystyle \angle AOC\)– прямой | \(\displaystyle \angle AON\)– тупой | \(\displaystyle \angle COD\)–развёрнутый. |