Развёрнутый угол \(\displaystyle AOG\) разделён на шесть острых углов.
Среди этих частей есть отмеченные на рисунке пары равных углов.
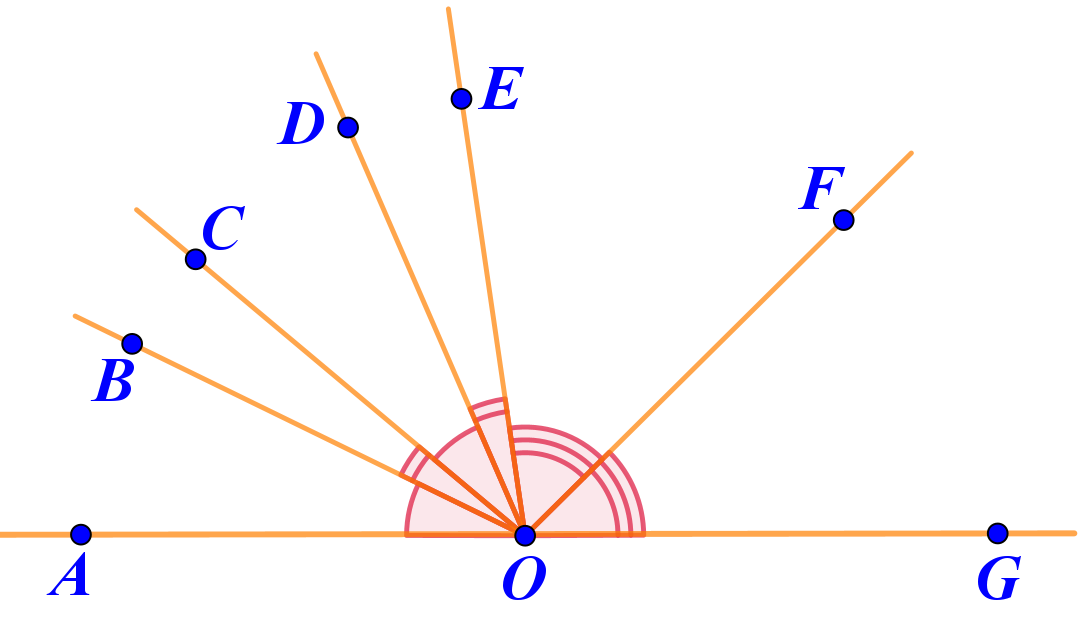
Найдите на рисунке прямой угол.
Угол |
Величины углов, изображенных на рисунке, могут быть любыми.
Единственный угол, величина которого известна \(\displaystyle -\) развёрнутый угол \(\displaystyle AOG\) величиной \(\displaystyle 180\degree {\small .}\)
Из \(\displaystyle 6\) углов, из которых составлен развёрнутый угол \(\displaystyle AOG{\small ,}\) можно выделить три пары равных углов:
\(\displaystyle \angle AOB=\angle COD{\small ,}\)\(\displaystyle \angle BOC=\angle DOE{\small ,}\)\(\displaystyle \angle EOF=\angle FOC{\small .}\)
То есть величина развёрнутого угла равна удвоенной сумме величин углов, обозначенных на рисунке одинарной, двойной и тройной дугами. Например:
\(\displaystyle 180\degree=2\cdot(\angle AOB+\angle BOC+\angle EOF){\small .}\)
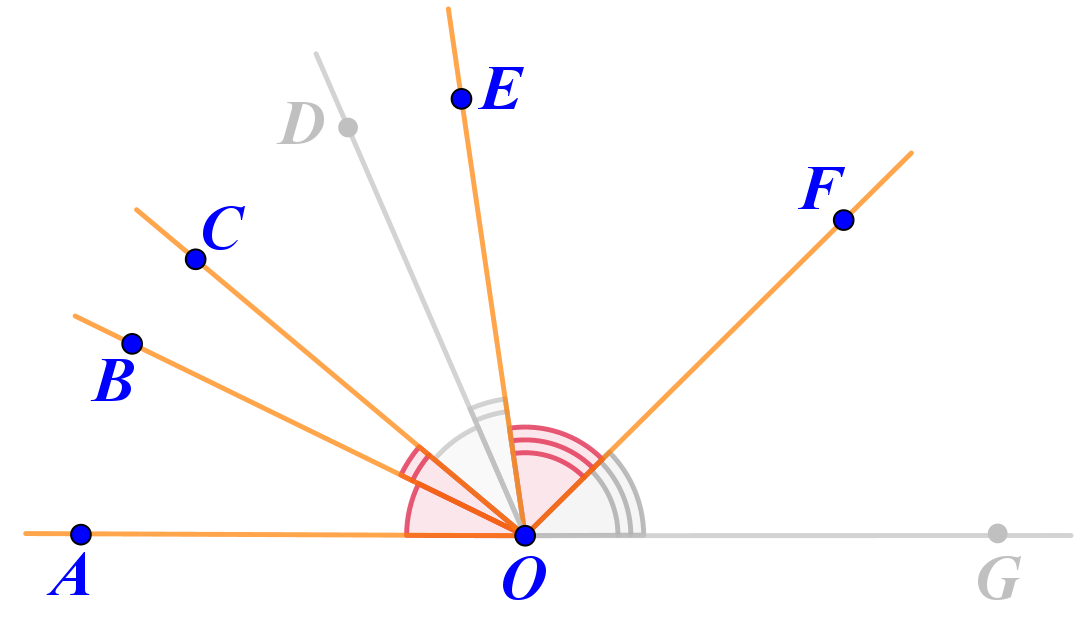
Разделим обе части равенства на два и поменяем местами:
\(\displaystyle \angle AOB+\angle BOC+\angle EOF=90\degree{\small .}\)
Это углы \(\displaystyle COD,\,DOE,\,EOF{\small .}\)
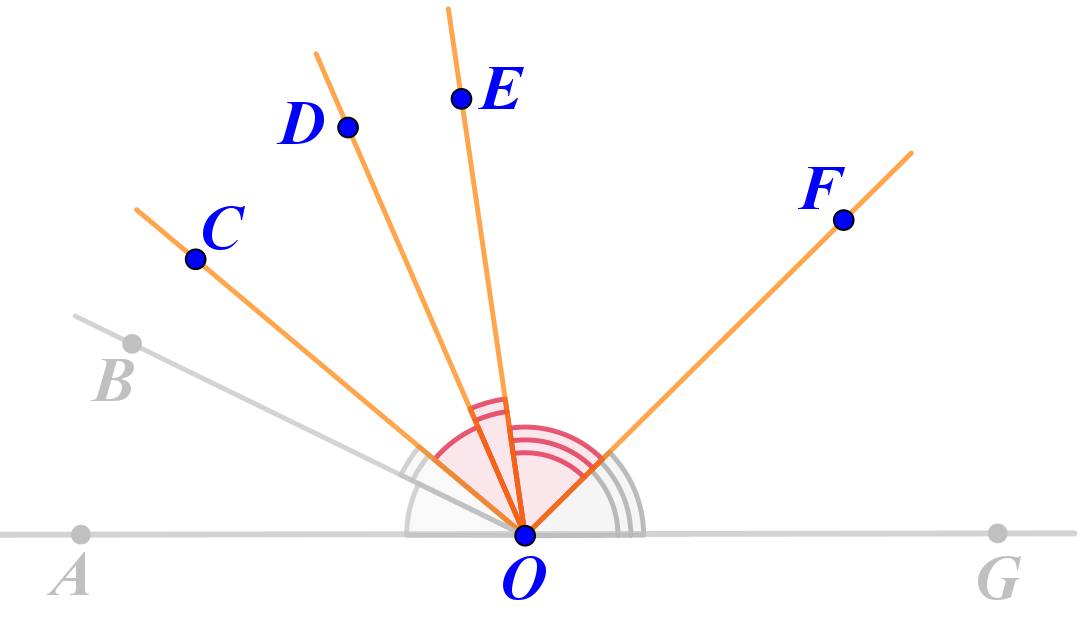
Поскольку эти углы равны соответственно углам \(\displaystyle AOB{\small ,\;}BOC\) и \(\displaystyle EOF{\small ,}\)то их величины равны величинам этих углов.
Значит, и сумма этих величин составляет \(\displaystyle 90\degree {\small .}\)
Угол \(\displaystyle COF\) составлен из этих углов. Значит, его величина равна \(\displaystyle 90\degree {\small ,}\) он прямой.
Альтернативное решение состоит в том, чтобы заметить, что лучи \(\displaystyle OC\) и \(\displaystyle OF\) являются биссектрисами смежных углов \(\displaystyle AOE\) и \(\displaystyle EOG\).
Поскольку сумма величин смежных углов равна \(\displaystyle 180\degree {\small ,}\) величина составленного из их половин угла равна \(\displaystyle 90\degree {\small .}\)
Биссектрисы смежных углов образуют прямой угол.
Ответ: \(\displaystyle \angle COF{\small .}\)