Два прямых угла имеют общую часть \(\displaystyle -\) угол величиной \(\displaystyle 21\degree {\small .}\)
Какова величина наибольшего угла, образованного сторонами этих прямых углов?
\(\displaystyle \degree \)
Угол называется прямым, если он равен смежному с ним углу.
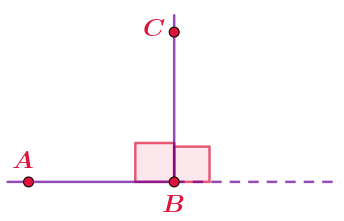
На рисунке прямой угол \(\displaystyle ABC\) и смежный с ним, равный ему прямой угол.
Прямые углы отмечаются специальным способом: в их внутренней области изображается квадрат, две стороны которого лежат на сторонах угла.
Величина прямого угла равна \(\displaystyle 90\degree {\small .}\)
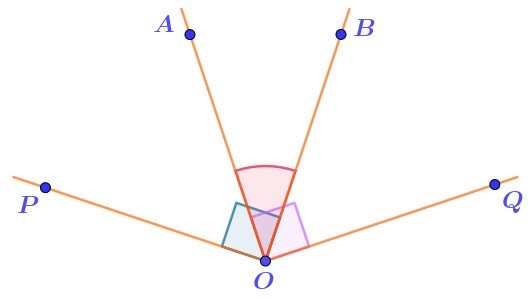
Начнём с угла \(\displaystyle AOB\) величиной \(\displaystyle 21\degree \) который является общей частью двух прямых углов.
Отложим прямой угол \(\displaystyle BOP\) от луча \(\displaystyle OB\) в ту же сторону, куда отложен угол \(\displaystyle AOB{\small .}\) Исходный угол станет частью прямого.
Отложим прямой угол \(\displaystyle AOQ\) от луча \(\displaystyle OA\) в ту же сторону, куда отложен угол \(\displaystyle AOB{\small .}\) Исходный угол станет частью прямого.
| \(\displaystyle \color{blue}{\angle AOP}=\angle BOP -\angle AOB=90\degree -21\degree =69\degree{\small .}\) | 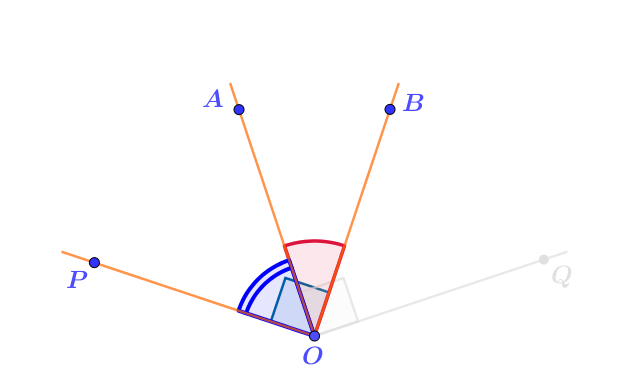 |
| \(\displaystyle \angle POQ=\angle AOP+\angle AOQ= 69\degree + 90\degree =159\degree{\small .}\) | 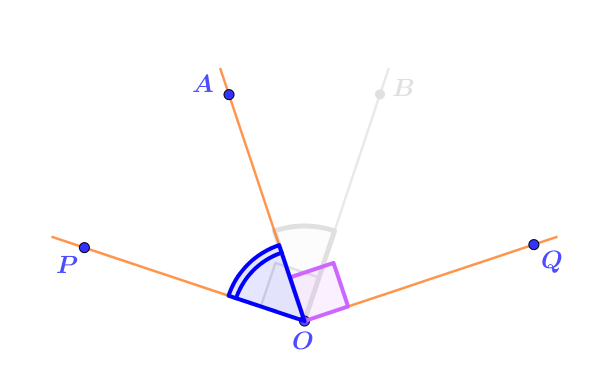 |
Ответ: \(\displaystyle 159\degree{\small .}\)