Семь лучей с общим началом образуют семь отмеченных на рисунке равных углов.
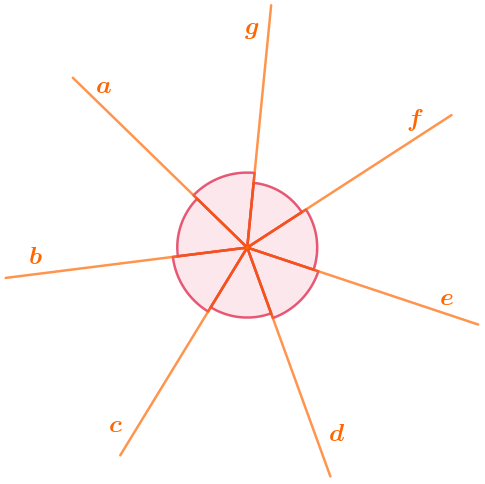
Сколько тупых углов можно обозначить, пользуясь обозначениями этих лучей?
Любой тупой угол будет составлен из отмеченных на рисунке равных углов.
Поэтому подсчет углов осуществим следующим образом:
- покажем, что отмеченные углы на рисунке являются острыми;
- посчитаем, сколько тупых углов можно составить из двух наименьших;
- посчитаем, сколько тупых углов можно составить из трех наименьших;
- покажем, что четыре наименьших угла не могут образовать тупой угол.
Проверяем это, пользуясь тем, что они равны и сумма их равных величин равна \(\displaystyle 360\degree{\small : } \)
\(\displaystyle \frac{360\degree }{7}<90\degree {\small .}\)
На рисунке угол \(\displaystyle ge\) составлен из двух острых углов \(\displaystyle gf\) и \(\displaystyle fe{\small .}\)
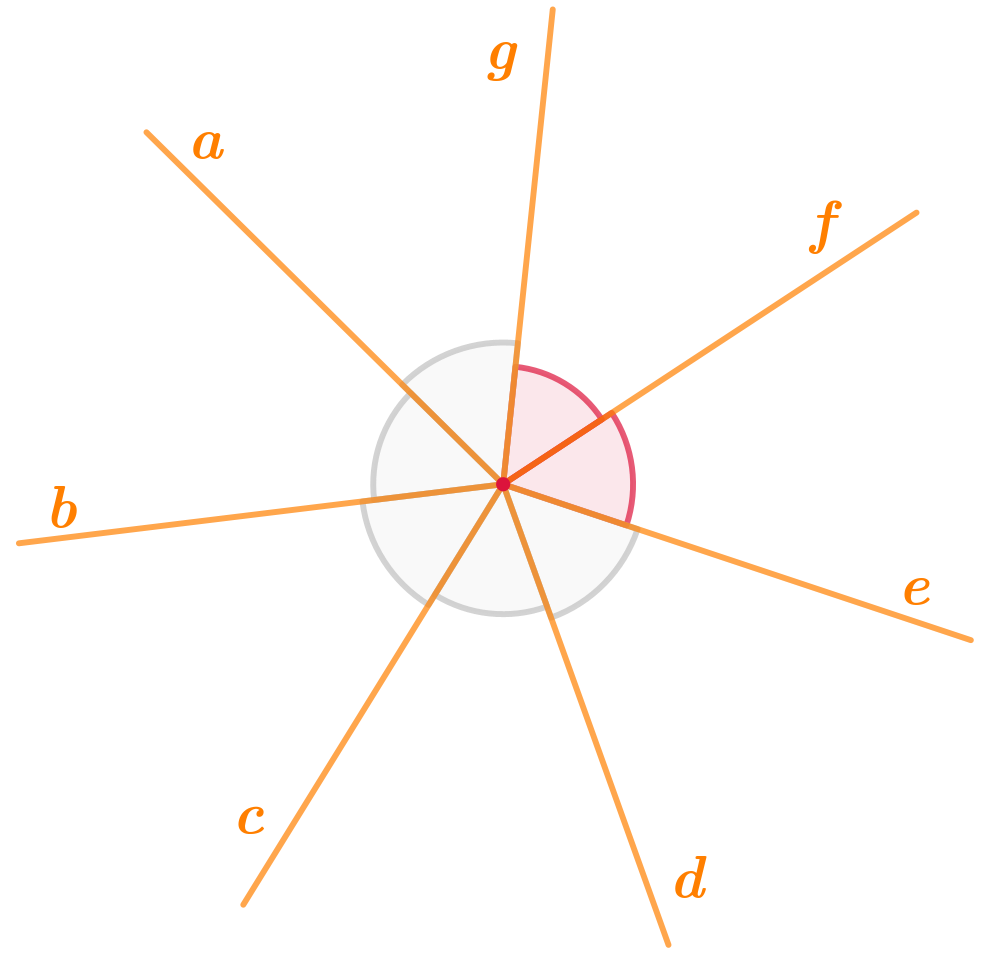
Проверим, что это тупой угол, оценив его величину:
\(\displaystyle 90\degree <2\cdot\frac{ 360\degree }{7}<180\degree {\small .}\)
Запишем все тупые углы, состоящие из двух острых углов, имеющих общую сторону:
\(\displaystyle \angle ge,\,\angle fd,\,\angle ec,\,\angle db,\,\angle ca,\,\angle bg,\,\angle af{\small .}\)
Получили \(\displaystyle 7\) тупых углов.
На рисунке тупой угол \(\displaystyle ae\) составлен из трёх острых углов \(\displaystyle ag,\,fg\) и \(\displaystyle fe{\small .}\)
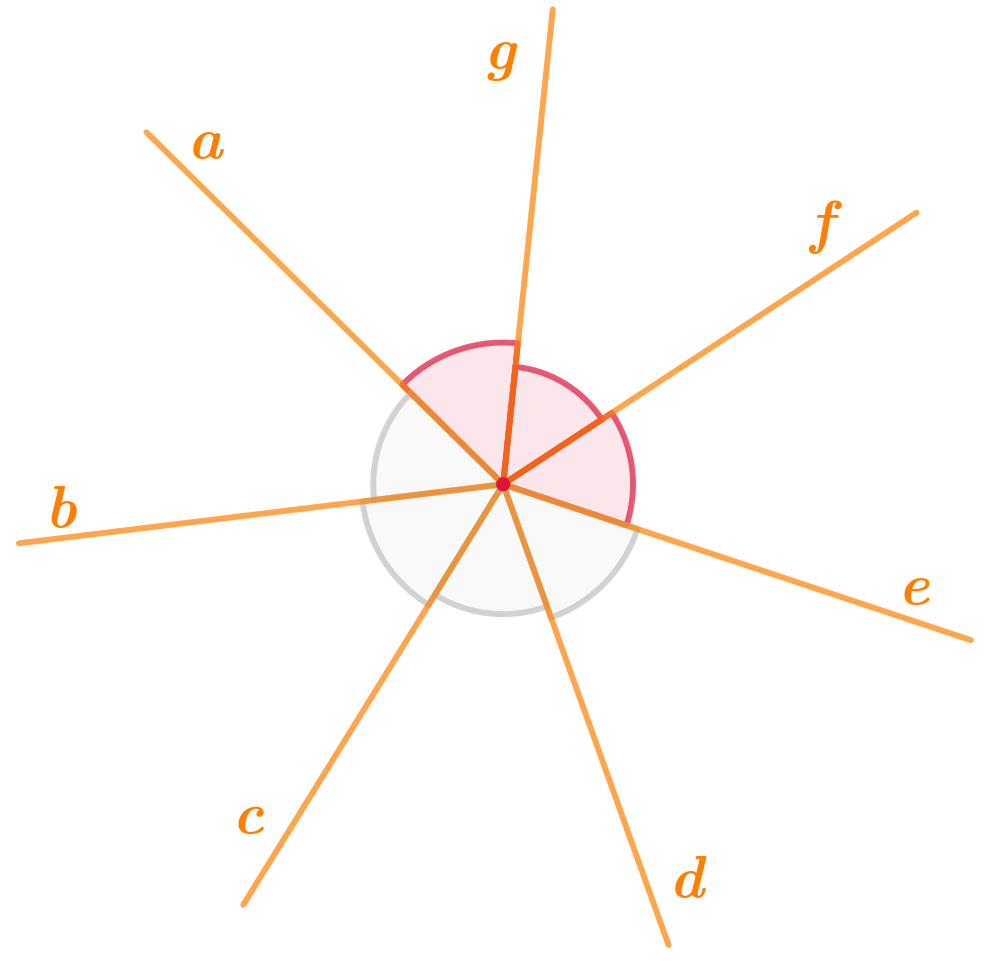
Проверим, что это тупой угол, оценив его величину:
\(\displaystyle 90\degree <3\cdot\frac{ 360\degree }{7}<180\degree {\small .}\)
Запишем все тупые углы, состоящие из трёх острых углов, и имеющих попарно общую сторону:
\(\displaystyle \angle ae,\,\angle gd,\,\angle fc,\,\angle eb,\,\angle da,\,\angle cg,\,\angle bf{\small .}\)
Получили ещё \(\displaystyle 7\) тупых углов.
В противном случае величина такого угла была бы равна:
\(\displaystyle 4\cdot\frac{ 360\degree }{7}>180\degree {\small .}\)
Но величина никакого угла не может быть большей, чем у развёрнутого.
Ответ: используя обозначения лучей, можно обозначить \(\displaystyle 14\) тупых углов.