На клетчатой бумаге изображён прямоугольный треугольник \(\displaystyle ABC{\small.}\)
На гипотенузе \(\displaystyle BC\) отмечена точка \(\displaystyle T{\small.}\)
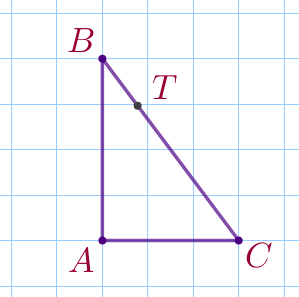
Укажите верное равенство.
Теорема Фалеса (о разбиении на равные отрезки)
Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут от второй прямой равные между собой отрезки.
тогда \(\displaystyle \color{green}{B_1B_2}=\color{green}{B_2B_3}=\color{green}{B_3B_4}=\color{green}{B_4B_5}{\small.}\) | 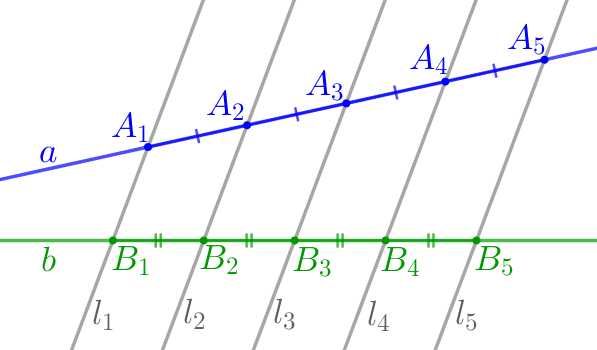 |
Заметим, что точка \(\displaystyle T\) лежит на горизонтальной линии сетки.
Выполним дополнительное построение.
По горизонтальным линиям сетки проведём параллельные прямые.
Эти прямые делят катет \(\displaystyle AB\) на четыре равных отрезка, каждый из которых равен стороне клетки. Согласно теореме Фалеса построенные прямые на гипотенузе \(\displaystyle BC\) также отсекают четыре равные между собой отрезка. \(\displaystyle BT\) – один из четырёх равных отрезков, которые составляют гипотенузу \(\displaystyle BC{\small,}\) значит, \(\displaystyle BT=\frac{1}{4}\cdot BC{\small.}\) | 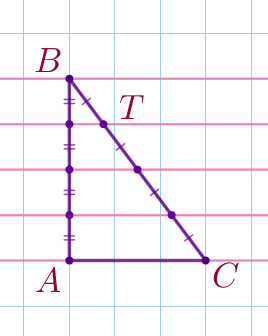 |
Ответ: \(\displaystyle BT=\frac{1}{4}\cdot BC{\small.}\)