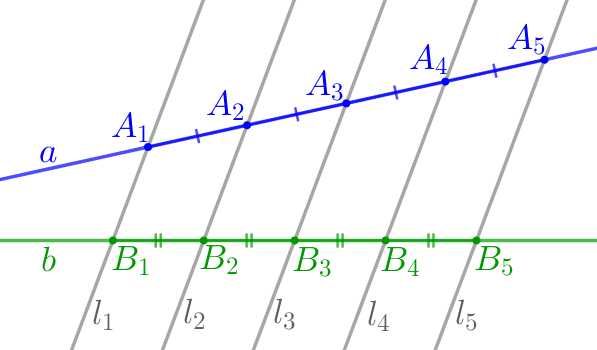
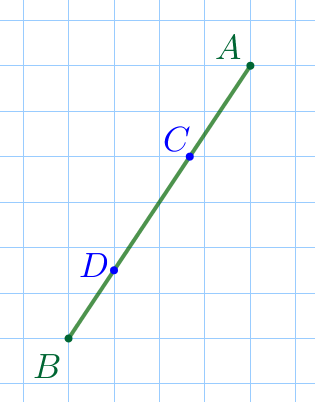
На клетчатой бумаге изображён отрезок \(\displaystyle AB{\small,}\) на котором отмечены точки \(\displaystyle C\) и \(\displaystyle D{\small.}\)
Найдите отношение \(\displaystyle CD:AB{\small,}\) если известно, что \(\displaystyle C\) и \(\displaystyle D\) лежат на линиях сетки.
\(\displaystyle CD:AB=\) \(\displaystyle :\)
Так как точки \(\displaystyle C\) и \(\displaystyle D\) лежат на отрезке \(\displaystyle AB{\small,}\) то
\(\displaystyle CD=AB-(AC+DB){\small.}\)
\(\displaystyle \color{red}{1)}\) Определим, какую часть отрезка \(\displaystyle AB\) составляет отрезок \(\displaystyle AC{\small.}\)
Заметим, что точка \(\displaystyle C\) лежит на пересечении отрезка \(\displaystyle AB\) и горизонтальной линии сетки.
Выполним дополнительное построение.
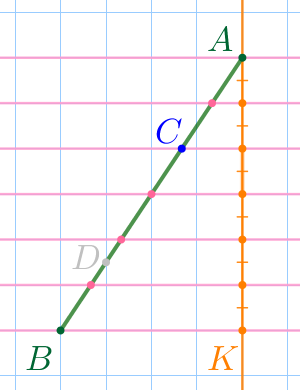 |
Горизонтальные параллельные прямые отсекают на прямой \(\displaystyle AK\) шесть равных отрезков. Каждый из этих отрезков равен стороне клетки. |
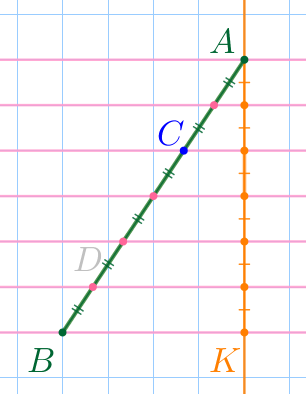 |
\(\displaystyle AC\) составляет две из шести равных частей, на которые разделили отрезок \(\displaystyle AB{\small,}\) то есть \(\displaystyle AC=\frac{2}{6}AB=\frac{1}{3}AB{\small.}\) |
\(\displaystyle \color{red}{2)}\) Определим, какую часть отрезка \(\displaystyle AB\) составляет отрезок \(\displaystyle DB{\small.}\)
Заметим, что точка \(\displaystyle D\) лежит на пересечении отрезка \(\displaystyle AB\) и вертикальной линии сетки.
Выполним дополнительное построение.
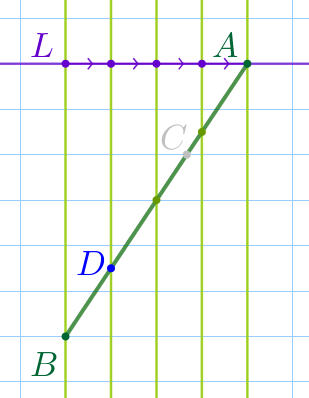 |
Вертикальные параллельные прямые отсекают на прямой \(\displaystyle AL\) четыре равных отрезка. Каждый из этих отрезков равен стороне клетки. |
Согласно теореме Фалеса построенные горизонтальные прямые делят отрезок \(\displaystyle AB\) на четыре равных между собой отрезка.
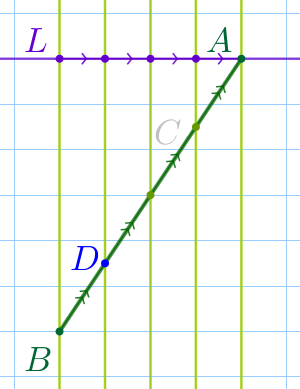 |
\(\displaystyle DB\) составляет одну из четырёх равных частей, на которые разделили отрезок \(\displaystyle AB{\small,}\) то есть \(\displaystyle DB=\frac{1}{4}AB{\small.}\) |
\(\displaystyle \color{red}{3)}\) Найдём отношение отрезков \(\displaystyle CD\) и \(\displaystyle AB{\small.}\)
Выразим \(\displaystyle CD\) через \(\displaystyle AB{\small:}\)
\(\displaystyle CD=AB-(AC+DB){\small;}\)
\(\displaystyle CD=AB-\left(\frac{1}{3}AB+\frac{1}{4}AB\right){\small;}\)
\(\displaystyle CD=AB-\frac{7}{12}AB{\small;}\)
\(\displaystyle CD=\frac{5}{12}AB{\small.}\)
Значит,
\(\displaystyle CD:AB=5:12{\small.}\)
Ответ: \(\displaystyle CD:AB=5:12{\small.}\)