На клетчатой бумаге изображён отрезок \(\displaystyle AB{\small,}\) на котором отмечены точки \(\displaystyle C{\small,}\) \(\displaystyle D\) и \(\displaystyle E{\small.}\)
Найдите отношение \(\displaystyle AC:DE{\small,}\) если известно, что \(\displaystyle C{\small,}\) \(\displaystyle D\) и \(\displaystyle E\) лежат на линиях сетки.
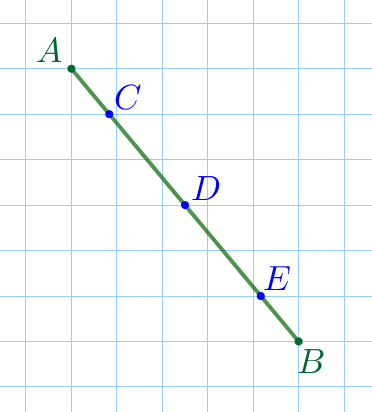
\(\displaystyle AC:DE=\) \(\displaystyle :\)
Заметим, что точки \(\displaystyle C{\small,}\) \(\displaystyle D\) и \(\displaystyle E\) лежат на пересечении отрезка \(\displaystyle AB\) и горизонтальных линий сетки.
Выполним дополнительное построение.
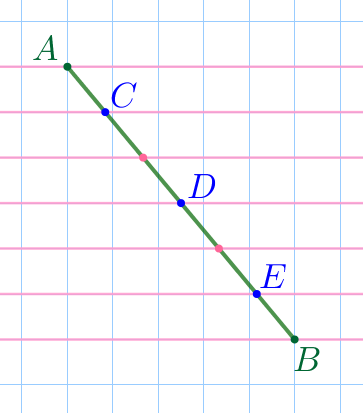 | Отметим все точки пересечения отрезка \(\displaystyle AB\) и горизонтальных линий сетки. Через отмеченные точки проведём горизонтальные параллельные прямые. |
Через точку \(\displaystyle A\) по вертикальной линии сетки проведём прямую \(\displaystyle AK{\small.}\)
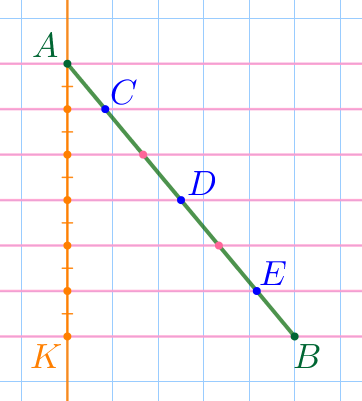 | По рисунку видим, что горизонтальные параллельные прямые отсекают на прямой \(\displaystyle AK\) шесть равных отрезков. Каждый из этих отрезков равен стороне клетки. |
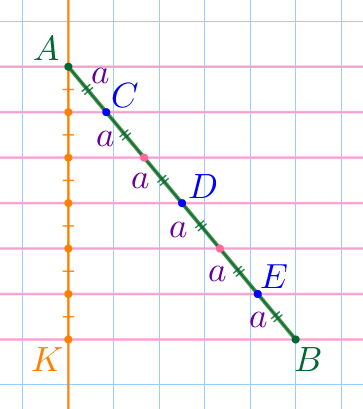 | Пусть \(\displaystyle a\) – длина каждого из шести равных отрезков, полученных при разбиении отрезка \(\displaystyle AB{\small.}\) По рисунку определяем: \(\displaystyle AC=a{\small;}\) \(\displaystyle DE=2a{\small.}\) |
Найдём отношение отрезков \(\displaystyle AC\) и \(\displaystyle DE{\small:}\)
\(\displaystyle AC:DE=a:2a=1:2{\small.}\)
Ответ: \(\displaystyle AC:DE=1:2{\small.}\)