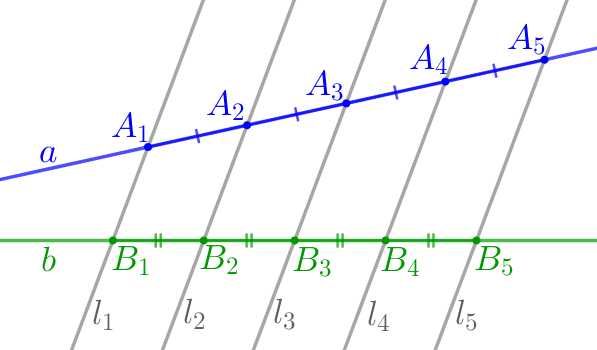
На клетчатой бумаге изображён треугольник \(\displaystyle ABC{\small,}\) на стороне \(\displaystyle BC\) которого отмечена точка \(\displaystyle V{\small.}\) Найдите отношение \(\displaystyle BV:VC{\small.}\)
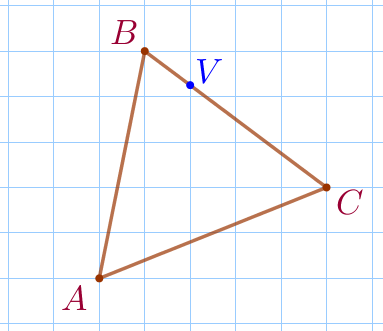
\(\displaystyle BV:VC=\) \(\displaystyle :\)
Заметим, что точка \(\displaystyle V\) лежит на пересечении стороны \(\displaystyle BC\) и вертикальной линии сетки.
Выполним дополнительное построение.
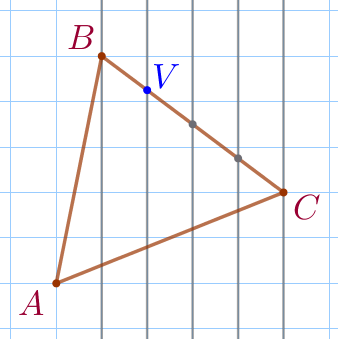 | Отметим все точки пересечения стороны \(\displaystyle BC\) и вертикальных линий сетки. Через отмеченные точки проведём вертикальные параллельные прямые. |
Точка \(\displaystyle B\) лежит на горизонтальной линии сетки.
Через точку \(\displaystyle B\) по горизонтальной линии сетки проведём луч \(\displaystyle BL{\small.}\)
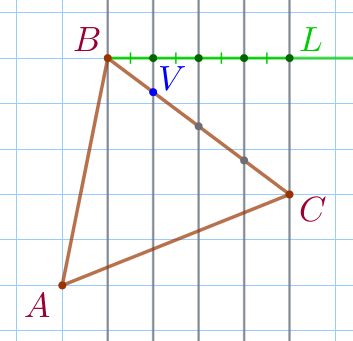 | По рисунку видим, что вертикальные параллельные прямые отсекают на луче \(\displaystyle BL\) четыре равных отрезка. Каждый из этих отрезков равен стороне клетки. |
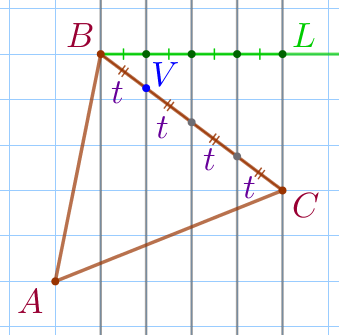 | Пусть \(\displaystyle t\) – длина каждого из четырёх равных отрезков, полученных при разбиении стороны \(\displaystyle BC{\small.}\) По рисунку определяем: \(\displaystyle BV=t{\small;}\) \(\displaystyle VC=3t{\small.}\) |
Найдём отношение отрезков \(\displaystyle BV\) и \(\displaystyle VC{\small:}\)
\(\displaystyle BV:VC=t:3t=1:3{\small.}\)
Ответ: \(\displaystyle BV:VC=1:3{\small.}\)