Skip to main content

Теория: 03 Признаки равенства треугольников

Задание

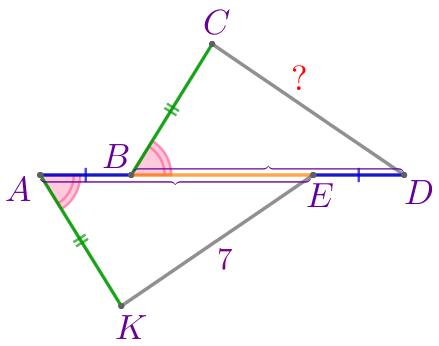
На отрезке \(\displaystyle AD\) взяли точки \(\displaystyle B\) и \(\displaystyle E\) так, что \(\displaystyle AB=ED{\small.}\) Точки \(\displaystyle C\) и \(\displaystyle K\) выбрали так, что \(\displaystyle BC=AK\) и равны углы \(\displaystyle CBD\) и \(\displaystyle KAE{\small.}\) Найдите длину отрезка \(\displaystyle CD{\small,}\) если \(\displaystyle EK=7{\small.}\)

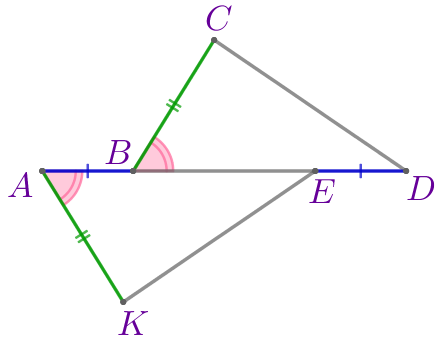
\(\displaystyle CD=\) 

Решение
  • \(\displaystyle AB=ED{\small;}\)
  • \(\displaystyle AK=BC{\small;}\)
  • \(\displaystyle \angle KAE= \angle CBD{\small;}\)
  • \(\displaystyle EK=7{\small.}\)

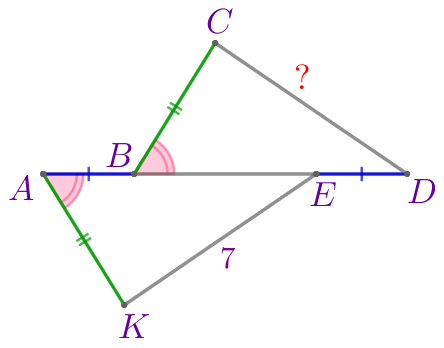Требуется найти \(\displaystyle CD{\small.}\)

Заметим, что

\(\displaystyle AE=BD{\small.}\)

Правило

Первый признак равенства треугольников

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Если

\(\displaystyle \begin{cases}\color{blue}{AB}=\color{blue}{A_1B_1}{\small,}\\\color{green}{AC}=\color{green}{A_1C_1}{\small,}\\\angle\color{red}{BAC}=\angle\color{red}{{B_1A_1C_1}}{\small,}\end{cases}\)

то

\(\displaystyle \Delta ABC=\Delta A_1B_1C_1{\small.}\)

Рассмотрим треугольники \(\displaystyle AKE\)  и \(\displaystyle BCD{\small.}\)

  • \(\displaystyle AE=BD{\small;}\)
  • \(\displaystyle AK=BC{\small;}\)
  • \(\displaystyle \angle KAE= \angle CBD{\small.}\)

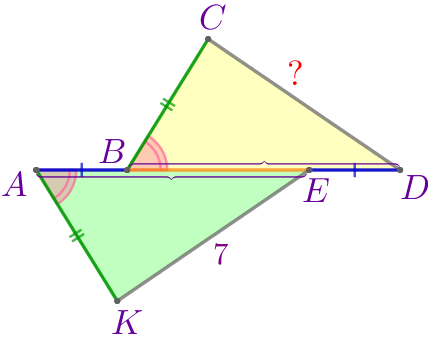Согласно признаку равенства треугольников

\(\displaystyle \triangle AKE=\triangle BCD\)

по двум сторонам и углу между ними.

В равных треугольниках напротив соответственно равных углов лежат равные стороны. Значит,

\(\displaystyle CD=EK=7{\small.}\)

Ответ: \(\displaystyle CD=7{\small.}\)