На сторонах \(\displaystyle AB{\small,}\) \(\displaystyle BC\) и \(\displaystyle AC\) равностороннего треугольника \(\displaystyle ABC\) отметили соответственно точки \(\displaystyle D{\small,}\) \(\displaystyle E\) и \(\displaystyle F\) так, что \(\displaystyle AD=BE=CF{\small.}\) \(\displaystyle L\) – точка пересечения отрезков \(\displaystyle AE\) и \(\displaystyle CD{\small,}\) \(\displaystyle M\) – точка пересечения отрезков \(\displaystyle AE\) и \(\displaystyle BF{\small,}\) \(\displaystyle N\) – точка пересечения отрезков \(\displaystyle BF\) и \(\displaystyle CD{\small.}\) Найдите \(\displaystyle MN\) и \(\displaystyle LN{\small,}\) если \(\displaystyle ML=9{\small.}\)
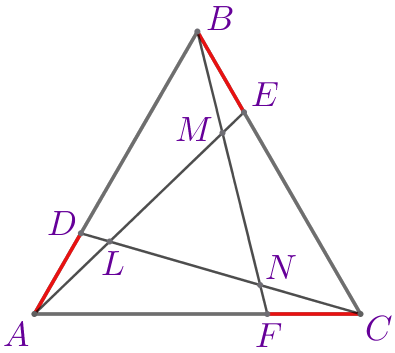
\(\displaystyle MN=\)\(\displaystyle {\small;}\) \(\displaystyle LN=\)\(\displaystyle {\small.}\)
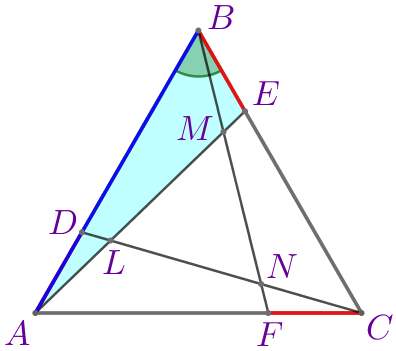 | 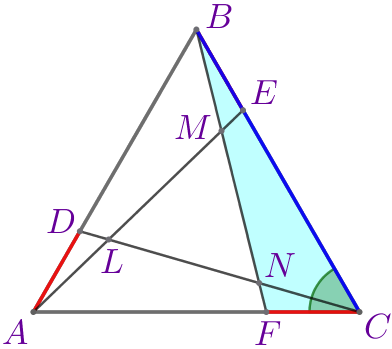 | 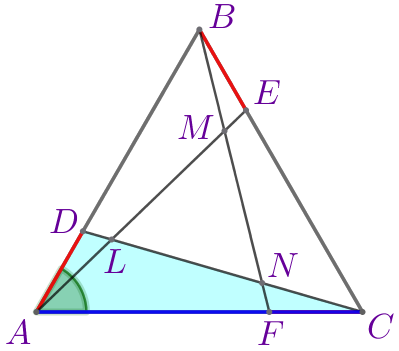 |
Следовательно, \(\displaystyle \triangle ABE=\triangle BCF=\triangle CAD\) по двум сторонам и углу между ними.
| ||
В равных треугольниках все соответственные элементы равны. | ||
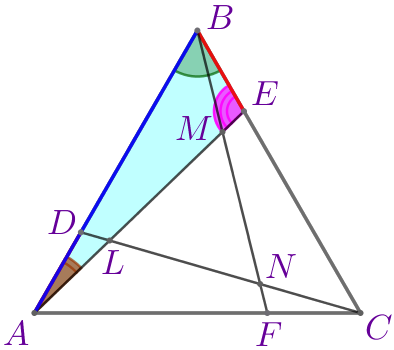 | 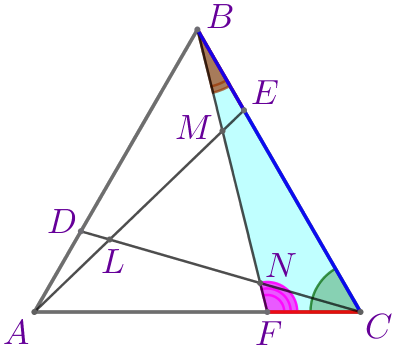 | 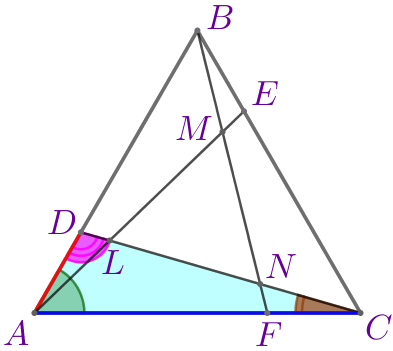 |
Значит, \(\displaystyle \color{brown}{\angle BAE}=\color{brown}{\angle CBF}=\color{brown}{\angle ACD}{\small;}\) \(\displaystyle \color{magenta}{\angle BEA}=\color{magenta}{\angle CFB}=\color{magenta}{\angle ADC}{\small.}\) | ||
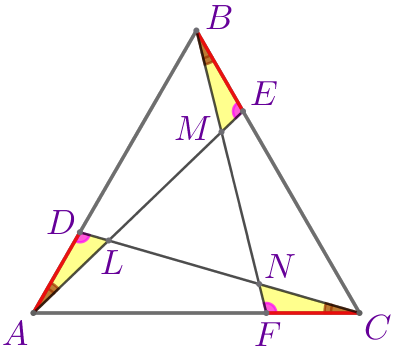 |
Следовательно, \(\displaystyle \triangle ADL=\triangle BEM=\triangle CFN\) по стороне и двум прилежащим к ней углам. |
Так как в равных треугольниках все соответственные элементы равны, то \(\displaystyle \color{blue}{\angle ALD}=\color{blue}{\angle BME}=\color{blue}{\angle CNF}{\small.}\) Тогда \(\displaystyle \color{blue}{\angle NLM}=\color{blue}{\angle LMN}=\color{blue}{\angle MNL}\) как вертикальные соответственно равным углам. | 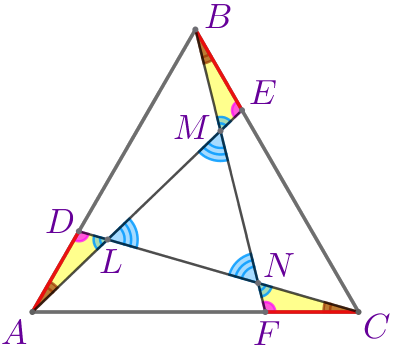 |
В результате получаем:
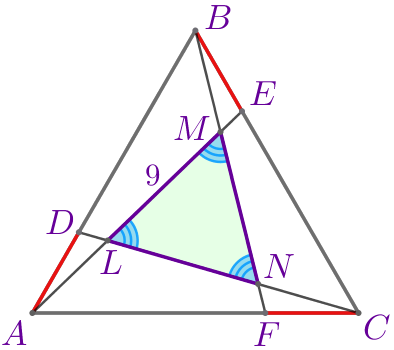 | В треугольнике \(\displaystyle LMN\) все углы равны. Следовательно, \(\displaystyle \triangle LMN\) – равносторонний. Значит, \(\displaystyle ML=MN=LN{\small.}\) |
По условию \(\displaystyle ML=9{\small,}\) тогда
\(\displaystyle MN=9{\small;}\) \(\displaystyle LN=9{\small.}\)
Ответ: \(\displaystyle MN=9{\small;}\) \(\displaystyle LN=9{\small.}\)