Теория: 06 Окружность

Задание

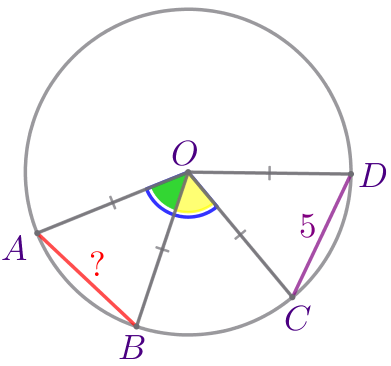
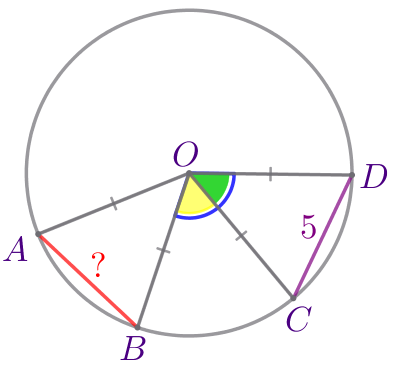
На рисунке изображена окружность с центром \(\displaystyle O{\small,}\) \(\displaystyle \angle AOC= \angle BOD{\small.}\) Найдите отрезок \(\displaystyle AB{\small,}\) если известно, что \(\displaystyle CD=5\, \footnotesize см{\small.}\)

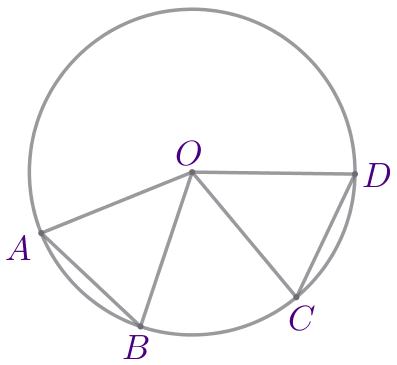
\(\displaystyle AB=\)\(\displaystyle \footnotesize см{\small.}\)

Решение

\(\displaystyle OA=OB=OC=OD\) – радиусы окружности;
\(\displaystyle \color{blue}{\angle AOC}= \color{blue}{\angle BOD}{\small;}\)
\(\displaystyle CD=5\, \footnotesize см{\small.}\)

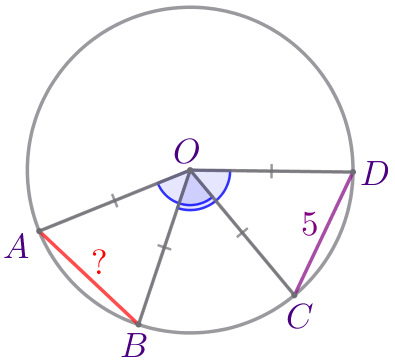Требуется найти длину отрезка \(\displaystyle AB{\small.}\)

Заметим, что

\(\displaystyle \color{green}{\angle AOB}=\color{green}{\angle COD}{\small.}\)

Вспомним первый признак равенства треугольников.

Рассмотрим треугольники \(\displaystyle AOB\) и \(\displaystyle COD{\small:}\)

\(\displaystyle OA=OC{\small;}\)
\(\displaystyle OB=OD{\small;}\)
\(\displaystyle \color{green}{\angle AOB}=\color{green}{\angle COD}{\small.}\)

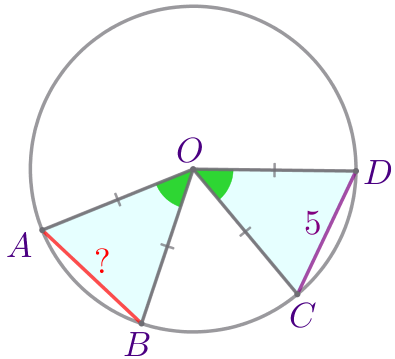Следовательно,

\(\displaystyle \triangle AOB= \triangle COD \)

по двум сторонам и углу между ними.

В равных треугольниках напротив соответственно равных углов лежат равные стороны. Значит,

\(\displaystyle AB=CD=5\, \footnotesize см{\small.}\)

Ответ: \(\displaystyle AB=5\, \footnotesize см{\small.}\)