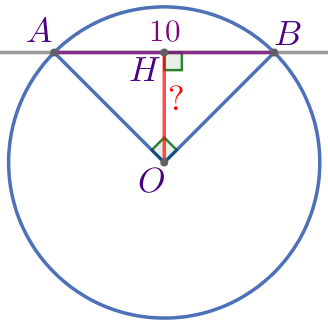
Дана окружность с центром в точке \(\displaystyle O{\small.}\) Прямая пересекает окружность в точках \(\displaystyle A\) и \(\displaystyle B{\small.}\) Найдите расстояние от точки \(\displaystyle O\) до прямой, если \(\displaystyle AB=10\, \footnotesize см{\small,}\) \(\displaystyle \angle AOB=90^{\circ}{\small.}\)
\(\displaystyle \footnotesize см{\small.}\)
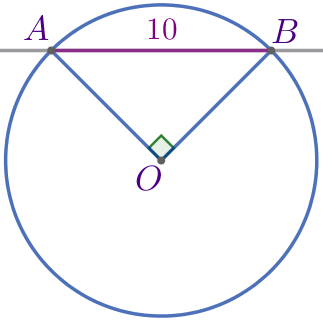 |
Требуется найти расстояние от точки \(\displaystyle O\) до прямой \(\displaystyle AB{\small.}\) |
Расстояние от точки до прямой равно длине перпендикуляра, проведённого от точки к данной прямой.
Из точки \(\displaystyle O\) проведём перпендикуляр \(\displaystyle OH\) к прямой \(\displaystyle AB{\small.}\) |
|
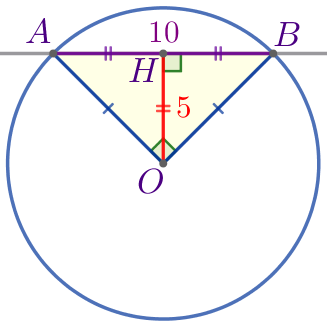 |
Следовательно, \(\displaystyle \triangle AOB\) – равнобедренный.
Значит, \(\displaystyle OH\) – высота и медиана, проведённая к гипотенузе. |
- В прямоугольном треугольнике медиана, проведённая к гипотенузе, равна половине гипотенузы. То есть
\(\displaystyle OH=\frac{1}{2} \cdot AB=\frac{1}{2} \cdot 10=5\, \footnotesize см{\small.}\)
Ответ: \(\displaystyle 5\, \footnotesize см{\small.}\)