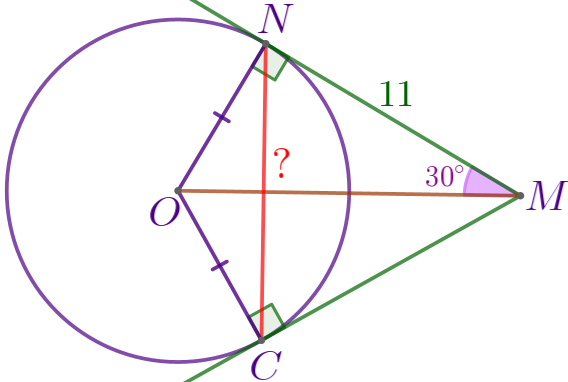
Прямые \(\displaystyle MN\) и \(\displaystyle MC\) касаются окружности с центром в точке \(\displaystyle O\) в точках \(\displaystyle N\) и \(\displaystyle C{\small.}\) Найдите \(\displaystyle NC{\small,}\) если \(\displaystyle \angle OMN=30^{\circ}{\small,}\) \(\displaystyle MN=11 \, \footnotesize см{\small.}\)
\(\displaystyle NC=\)\(\displaystyle \footnotesize см{\small.}\)
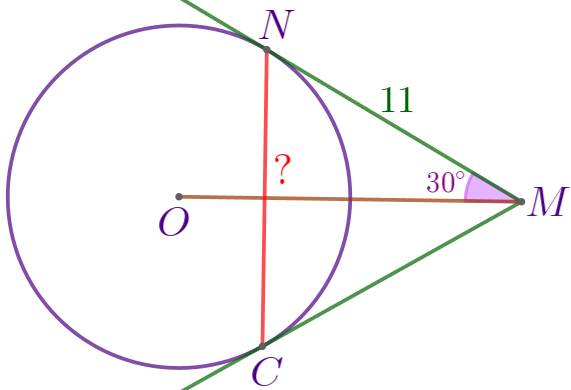 |
Требуется найти длину отрезка \(\displaystyle NC{\small.}\) |
Проведём радиусы \(\displaystyle ON\) и \(\displaystyle OC{\small.}\) Радиус, проведённый в точку касания, перпендикулярен касательной. Значит, \(\displaystyle \angle ONM=90^{\circ}{\small;}\) \(\displaystyle \angle OCM=90^{\circ}{\small.}\) |
|
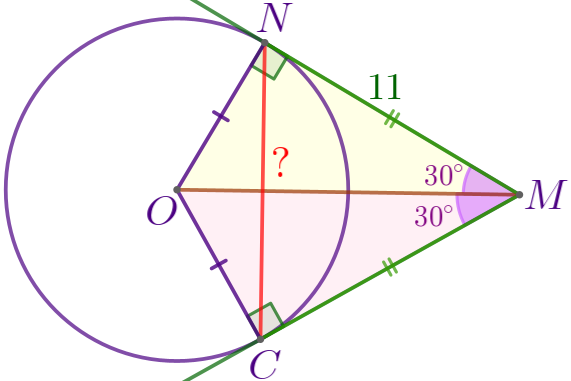 |
Следовательно, \(\displaystyle \triangle OMN= \triangle OMC\) по катету и гипотенузе. Значит, \(\displaystyle MC=MN=11{\small;}\) \(\displaystyle \angle OMC=\angle OMN=30^{\circ}{\small.}\) |
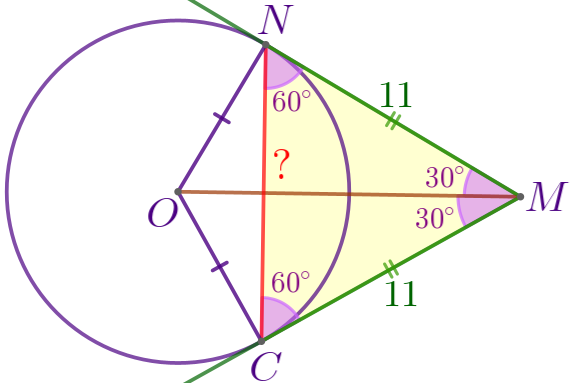 | \(\displaystyle \angle NMC=30^{\circ}+30^{\circ}=60^{\circ}{\small.}\)
Следовательно, \(\displaystyle \angle MNC=\angle MCN=\frac{180^{\circ}-\angle NMC}{2}{\small;}\) |
\(\displaystyle \angle MNC=\angle MCN=\frac{180^{\circ}-60^{\circ}}{2}=\frac{120^{\circ}}{2}=60^{\circ}{\small.}\)
В результате получаем:
\(\displaystyle \angle MNC=\angle MCN=\angle NMC=60^{\circ}{\small.}\)
То есть \(\displaystyle \triangle MNC\) – равносторонний. Значит,
\(\displaystyle NC=MC=MN=11{\small.}\)
Ответ: \(\displaystyle NC=11{\small.}\)