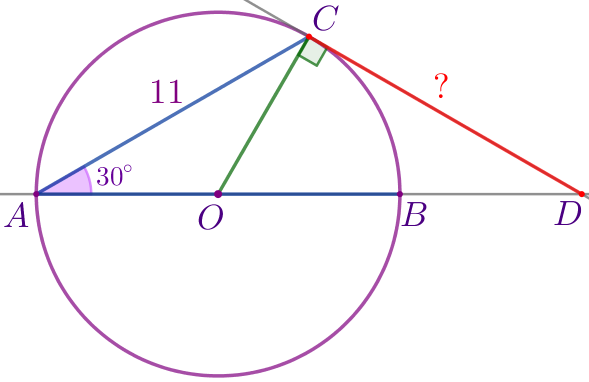
Угол между диаметром \(\displaystyle AB\) и хордой \(\displaystyle AC\) равен \(\displaystyle 30^{\circ}{\small.}\) Через точку \(\displaystyle C\) проведена касательная, пересекающая прямую \(\displaystyle AB\) в точке \(\displaystyle D{\small.}\) Найдите длину отрезка \(\displaystyle CD{\small,}\) если \(\displaystyle AC=11{\small.}\)
\(\displaystyle CD=\)
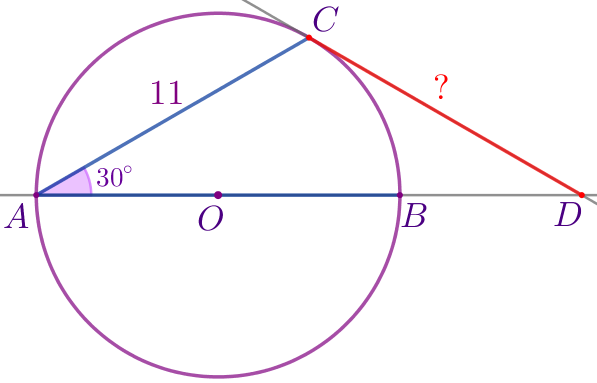 |
Требуется найти длину отрезка \(\displaystyle CD{\small.}\) |
Проведём радиус \(\displaystyle OC{\small.}\) Радиус, проведённый в точку касания, перпендикулярен касательной. Значит, \(\displaystyle \angle OCD=90^{\circ}{\small.}\) |
|
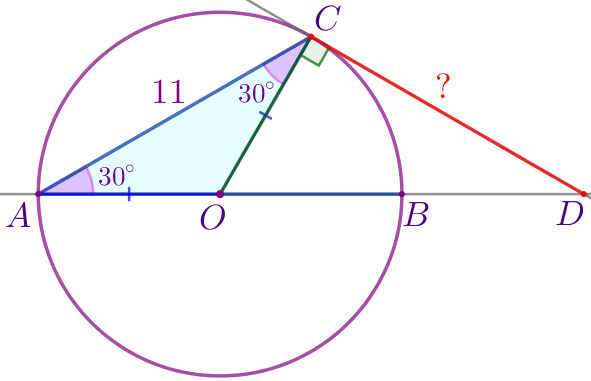 | \(\displaystyle OA=OC\) – радиусы окружности. Значит, \(\displaystyle \triangle AOC\) – равнобедренный. В равнобедренном треугольнике углы при основании равны. То есть \(\displaystyle \angle OCA=\angle OAC=30^{\circ}{\small.}\) |
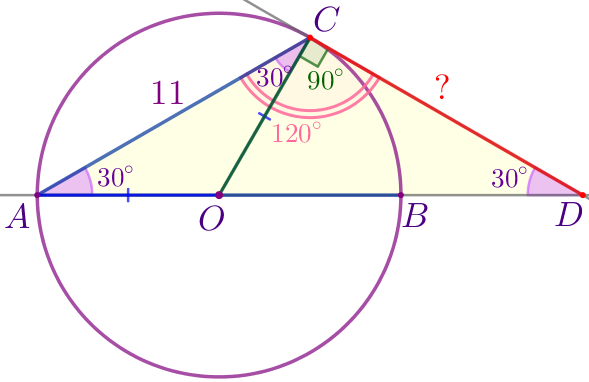 | \(\displaystyle \angle ACD=\angle OCA+\angle OCD{\small;}\) \(\displaystyle \angle ACD=30^{\circ}+90^{\circ}=120^{\circ}{\small.}\) Сумма внутренних углов треугольника равна \(\displaystyle 180^{\circ}{\small,}\) значит, \(\displaystyle \angle CDA=180^{\circ}-(\angle CAD+\angle ACD){\small;}\) \(\displaystyle\begin{aligned}\angle CDA&=180^{\circ}-(30^{\circ}+120^{\circ})=\\&=180^{\circ}-150^{\circ}=30^{\circ}{\small.}\end{aligned}\) |
В результате получаем
\(\displaystyle \angle CAD= \angle CDA=30^{\circ}{\small.}\)
Следовательно, \(\displaystyle \triangle ACD\) – равнобедренный. Значит,
\(\displaystyle CD=CA=11{\small.}\)
Ответ: \(\displaystyle CD=11{\small.}\)