Задание
Существует ли треугольник со сторонами \(\displaystyle 1{\small,}\) \(\displaystyle 2\) и \(\displaystyle 3{\small?}\)
Решение
Правило
Неравенство треугольника
Каждая сторона треугольника меньше суммы двух других сторон: \(\displaystyle AB<AC+CB\) \(\displaystyle AC<AB+BC\) \(\displaystyle BC<BA+AC\) |  |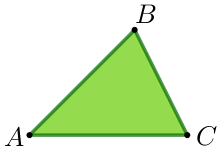
Пусть \(\displaystyle 1{\small,}\) \(\displaystyle 2\) и \(\displaystyle 3\) – стороны треугольника.
Проверим выполнение неравенства треугольника для каждой стороны:
\(\displaystyle 1<2+3\) – верно;
\(\displaystyle 2<1+3\) – верно;
\(\displaystyle 3<2+1\) – неверно.
Значит, не существует треугольника со сторонами \(\displaystyle 1{\small,}\) \(\displaystyle 2\) и \(\displaystyle 3{\small.}\)
Ответ: Нет.