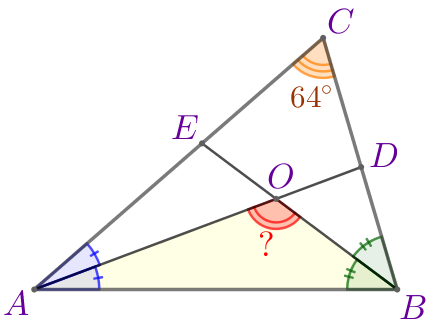
В треугольнике \(\displaystyle ABC\) \(\displaystyle \angle C=64^{\circ}{\small , }\) \(\displaystyle AD\) и \(\displaystyle BE\) – биссектрисы, пересекающиеся в точке \(\displaystyle O{\small .}\)
Найдите угол \(\displaystyle AOB{\small .}\) Ответ дайте в градусах.
\(\displaystyle \angle AOB=\)\(\displaystyle ^{\circ}{\small.}\)
\(\displaystyle ABC\) – треугольник:
Требуется найти угол \(\displaystyle AOB{\small.}\) | 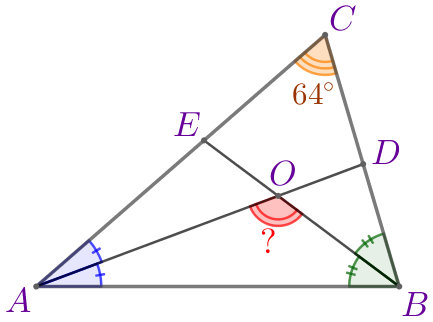 |
\(\displaystyle \color{red}{\angle AOB}=180^{\circ}-(\angle OAB+\angle OBA)\)
Введём обозначения. Пусть \(\displaystyle \angle BAD=\angle DAC=\color{blue}{\alpha}{\small , } \) \(\displaystyle \angle ABE=\angle EBC=\color{green}{\beta}{\small .} \) Значит, \(\displaystyle \angle A=2 \color{blue}{\alpha}{\small,}\) \(\displaystyle \angle B=2 \color{green}{\beta}{\small.}\) | 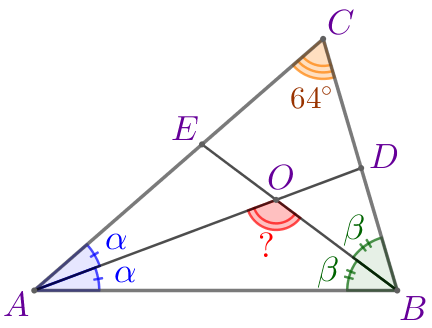 |
Тогда
\(\displaystyle \color{red}{\angle AOB}=180^{\circ}-(\angle OAB+\angle OBA)=180^{\circ}-(\color{blue}{\alpha}+\color{green}{\beta}){\small.}\)
Так как сумма внутренних углов треугольника равна \(\displaystyle 180^\circ{\small , } \) то в треугольнике \(\displaystyle ABC{\small:}\)
\(\displaystyle \angle A+ \angle B+ \angle C= 180^\circ{\small , } \)
то есть
\(\displaystyle 2\color{blue}{\alpha}+2 \color{green}{\beta}+64^\circ= 180^\circ{\small .} \)
Получаем
\(\displaystyle 2\color{blue}{\alpha}+2 \color{green}{\beta}= 180^{\circ}-64^{\circ}{\small;} \)
\(\displaystyle 2\cdot (\color{blue}{\alpha}+\color{green}{\beta})= 116^{\circ}{\small;} \)
\(\displaystyle \color{blue}{\alpha}+\color{green}{\beta}= 58^{\circ}{\small.} \)
В результате получаем
\(\displaystyle \color{red}{\angle AOB}=180^{\circ}-(\color{blue}{\alpha}+\color{green}{\beta})=180^{\circ}-58^{\circ}=122^{\circ}{\small.}\)
Ответ: \(\displaystyle \angle AOB=122^{\circ} {\small . } \)