Задание
На прямой \(\displaystyle AB\) отмечены несколько точек в показанном на рисунке порядке.
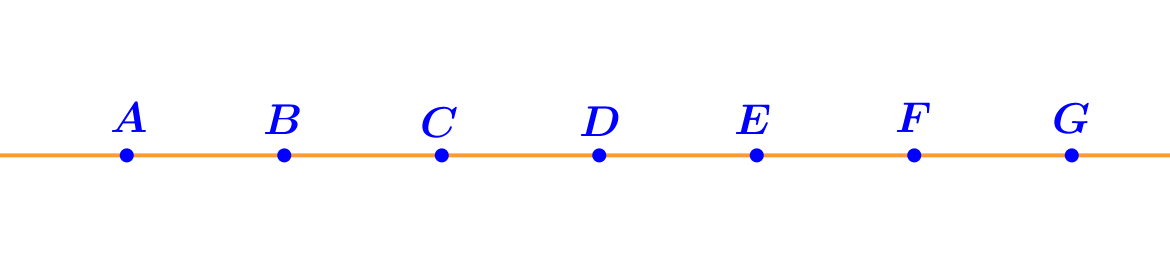
Какие из них удовлетворяют одновременно двум условиям:
- лежат между точками \(\displaystyle A\) и \(\displaystyle F{\small ,}\)
- но не лежат между точками \(\displaystyle B\) и \(\displaystyle D{\text ?}\)
Решение
Точка лежит между двумя данными точками, если является внутренней точкой отрезка с концами в этих точках.
Порядок точек на прямой
Чтобы убедиться, что точка лежит между двумя другими, следует проверить, что она принадлежит отрезку с концами в этих точках.
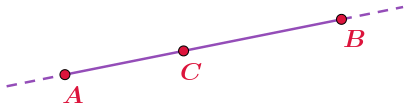
На рисунке точка \(\displaystyle C\) лежит между точками \(\displaystyle A\) и \(\displaystyle B{\small .}\)
- Внутренние точки отрезка и только они лежат между концами этого отрезка.
- Если точка лежит между двумя другими, то все три точки принадлежат одной прямой.
- Из трёх разных точек одной прямой ровно одна лежит между двумя другими.
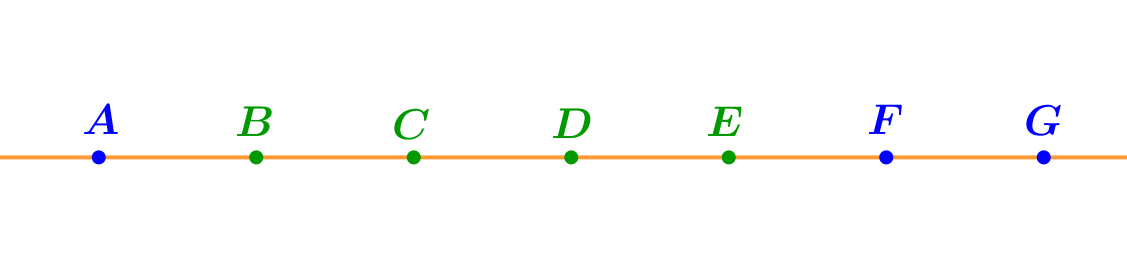
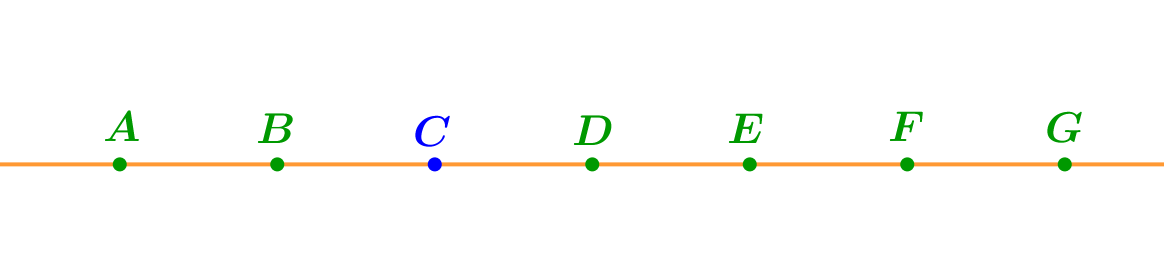
Выделим на двух рисунках точки, удовлетворяющие соответственно двум требованиям условия задачи.
- являются внутренними точками отрезка \(\displaystyle AF{\small ;}\)
- не являются внутренними точками отрезка \(\displaystyle BD{\small .}\)
Отберём обозначения точек, выделенных и на том, и на другом рисунках:
\(\displaystyle B,\,D,\,E{\small .}\)
Ответ: точки \(\displaystyle B,\,D,\,E{\small .}\)