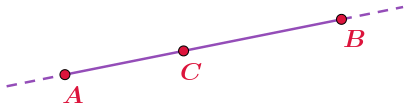
На отрезке отмечено несколько точек.

Сколько пар отмеченных точек таковы, что точка \(\displaystyle C\) лежит между точками, составляющими пару?
Перечисление одних и тех же двух точек в разном порядке описывает только одну пару.
Для этого две точки пары должны располагаться на прямой по разные стороны точки \(\displaystyle C{\small .}\)
Значит, одна из точек пары выбирается из двух точек \(\displaystyle A\) и \(\displaystyle B{\small .}\) Другая \(\displaystyle -\) из точек \(\displaystyle D{\small ,\;}E{\small ,\;}F\) и \(\displaystyle G{\small .}\)

Первый выбор осуществляется двумя способами, второй, независимо от первого \(\displaystyle -\) четырьмя.
Получается, что общее число пар должно быть равно \(\displaystyle 2\cdot 4=\)\(\displaystyle 8{\small .}\)
На всякий случай выпишем все подходящие пары и убедимся, что их восемь:
| \(\displaystyle A,D\) | \(\displaystyle A,E\) | \(\displaystyle A,F\) | \(\displaystyle A,G\) |
| \(\displaystyle B,D\) | \(\displaystyle B,E\) | \(\displaystyle B,F\) | \(\displaystyle B,G\) |
Ответ. \(\displaystyle 8{\small .}\)