Задание
Найдите длину вектора \(\displaystyle \overrightarrow{AB}\small,\) если длина стороны клетки \(\displaystyle 1\)см.
\(\displaystyle \left|\overrightarrow{AB}\right|=\)
см
Решение
Информация
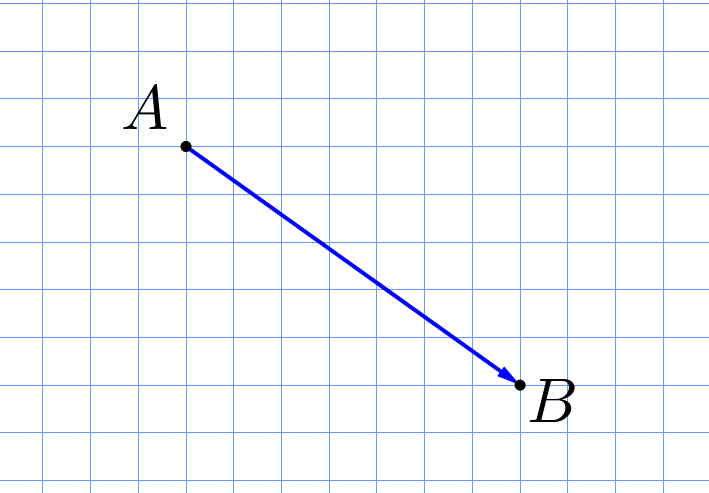
Длиной вектора \(\displaystyle \overrightarrow{AB}\) называется длина отрезка \(\displaystyle AB\small.\)
Чтобы найти длину вектора \(\displaystyle \overrightarrow{AB}\small,\) найдем длину отрезка \(\displaystyle AB\small.\) Отрезок \(\displaystyle AB\) – гипотенуза прямоугольного треугольника с катетами \(\displaystyle 5\)см и \(\displaystyle 7\)см. По теореме Пифагора: \(\displaystyle AB^2=5^2+7^2=74\) \(\displaystyle AB=\sqrt{74}\)см. Значит, \(\displaystyle |\overrightarrow{AB}|=AB=\sqrt{74}\)см. | 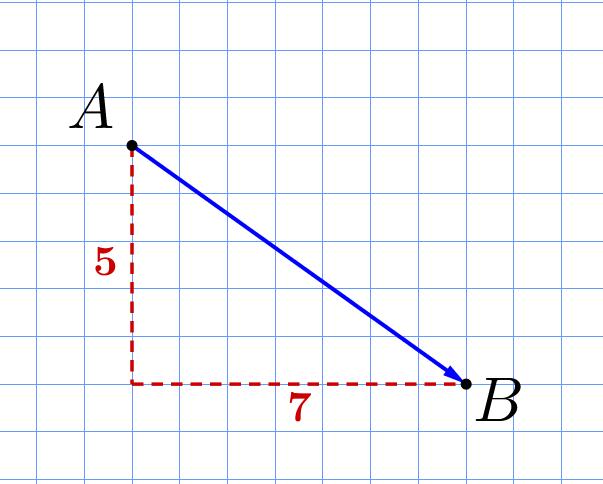 |