Какой вид имеет четырехугольник \(\displaystyle ABCD\small,\) если \(\displaystyle \overrightarrow{AD}=\overrightarrow{BC}?\)
Два вектора равны, если они сонаправлены и их длины равны.
По условию \(\displaystyle \overrightarrow{AD}=\overrightarrow{BC}\small.\) Тогда \(\displaystyle \overrightarrow{AD}\) и \(\displaystyle \overrightarrow{BC}\) сонаправлены и их длины равны.
1. Векторы \(\displaystyle \overrightarrow{AD}\) и \(\displaystyle \overrightarrow{BC}\) сонаправлены. Тогда
| 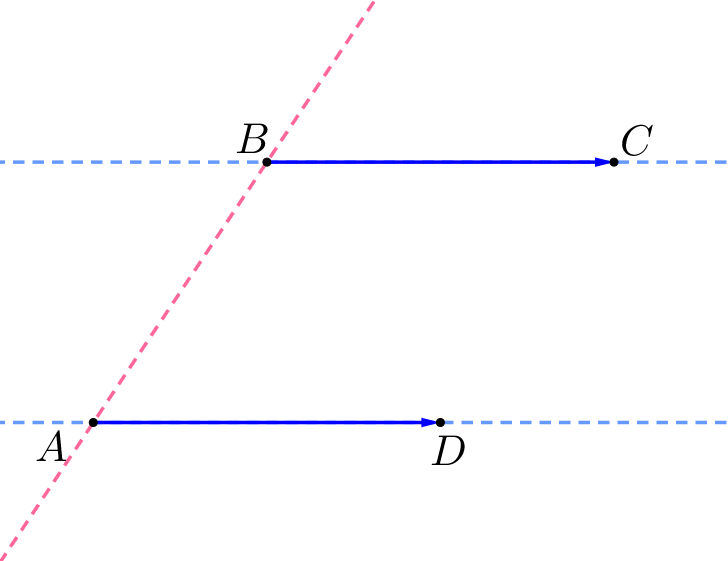 |
2. Длины векторов \(\displaystyle \overrightarrow{AD}\) и \(\displaystyle \overrightarrow{BC}\) равны. То есть
Тогда в четырехугольнике \(\displaystyle ABCD\) противоположные стороны \(\displaystyle AD\) и \(\displaystyle BC\) параллельны и равны. То есть \(\displaystyle ABCD\) – параллелограмм. | 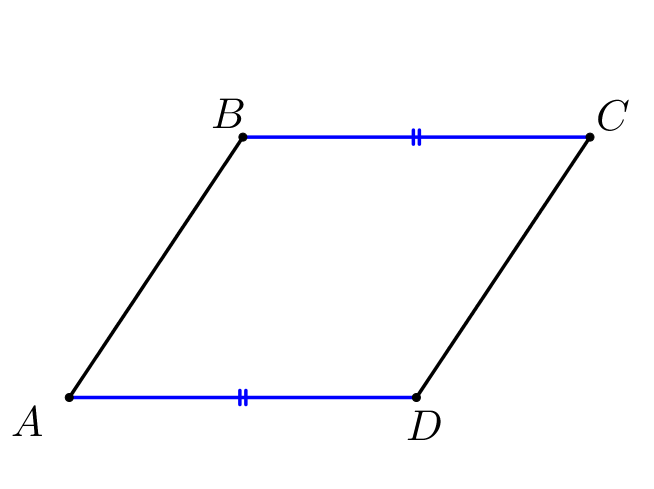 |
Ответ: \(\displaystyle ABCD\) – параллелограмм.