Диагонали параллелограмма \(\displaystyle ABCD\) пересекаются в точке \(\displaystyle O\small.\) Составьте верные равенства:
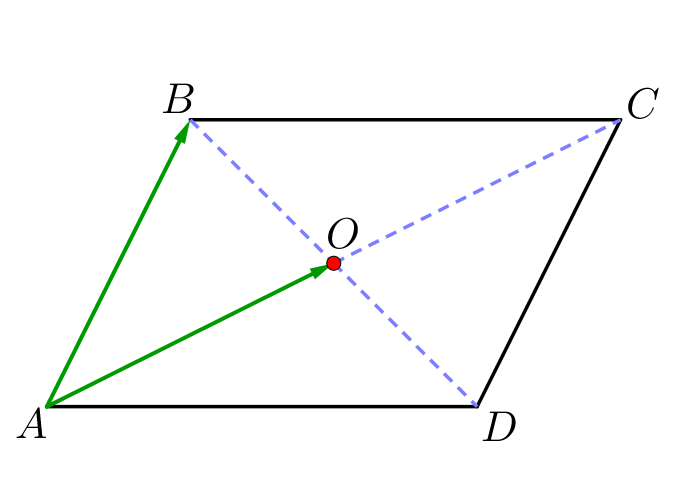
\(\displaystyle \overrightarrow{AB}=\)
\(\displaystyle \overrightarrow{AO}=\)
Два вектора равны, если они сонаправлены, и их длины равны.
\(\displaystyle \overrightarrow{AB}=\overrightarrow{DC}\small.\)
1. Выберем из предложенных векторов сонаправленные с \(\displaystyle \overrightarrow{AB}{\small.}\)
В параллелограмме противоположные стороны параллельны. Тогда из предложенных вариантов вектор \(\displaystyle \overrightarrow{AB}\) коллинеарен векторам \(\displaystyle \overrightarrow{CD}\) и \(\displaystyle \overrightarrow{DC}\small.\) При этом \(\displaystyle \overrightarrow{AB}\) сонаправлен только с вектором \(\displaystyle \overrightarrow{DC}\small.\) | 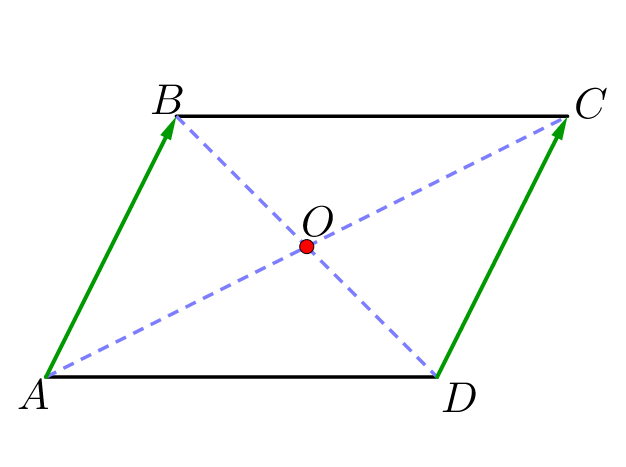 |
2. Противоположные стороны параллелограмма равны. То есть длины векторов \(\displaystyle \overrightarrow{AB}\) и \(\displaystyle \overrightarrow{DC}\) равны.
Значит,
\(\displaystyle \overrightarrow{AB}=\overrightarrow{DC}\small.\)
\(\displaystyle \overrightarrow{AO}=\overrightarrow{OC}\small.\)
1. Выберем из предложенных векторов сонаправленные с \(\displaystyle \overrightarrow{AO}{\small.}\)
Векторы \(\displaystyle AO\) и \(\displaystyle OC\) лежат на одной прямой. Тогда из предложенных вариантов вектор \(\displaystyle \overrightarrow{AO}\) коллинеарен вектору \(\displaystyle \overrightarrow{OC}\small.\) При этом они сонаправлены. | 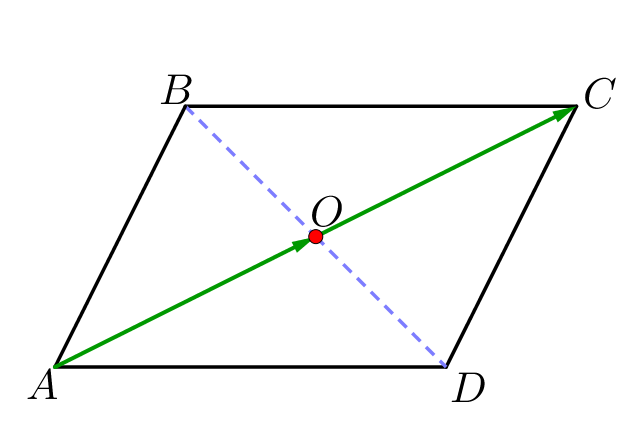 |
2. Диагонали параллелограмма делятся точкой пересечения пополам. То есть длины векторов \(\displaystyle \overrightarrow{AO}\) и \(\displaystyle \overrightarrow{OC}\) равны.
Значит,
\(\displaystyle \overrightarrow{AO}=\overrightarrow{OC}\small.\)
Ответ: \(\displaystyle \overrightarrow{AB}=\overrightarrow{DC}\) и \(\displaystyle \overrightarrow{AO}=\overrightarrow{OC}\small.\)