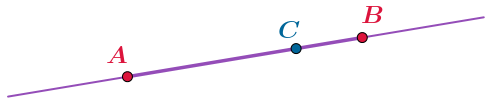
Точки \(\displaystyle A{\small ,\;}B\) и \(\displaystyle C\) принадлежат одной прямой. Известны длины отрезков \(\displaystyle AB=11\) и \(\displaystyle BC=3{\small .}\)
Какие значения может принимать длина отрезка \(\displaystyle AC{\text ?}\)
Из трёх точек прямой ровно одна лежит между двумя другими.
Разберём три случая, в которых на эту роль претендуют обозначения \(\displaystyle A{\small ,\;}B\) и \(\displaystyle C{\small .}\)
Иначе отрезок \(\displaystyle AB\) был бы частью отрезка \(\displaystyle BC{\small .}\)
Но по условию его длина равна \(\displaystyle 11{\small ,}\) он длиннее отрезка \(\displaystyle BC\) длиной \(\displaystyle 3{\small .}\)
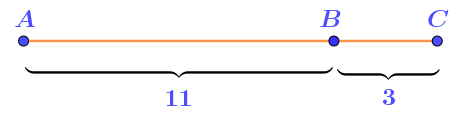
По правилу для расстояний между точками прямой можно записать равенство:
\(\displaystyle AB+BC=AC{\small .}\)
Подставляя данные задачи, получим:
\(\displaystyle AC=11+3=\)\(\displaystyle 14{\small .}\)
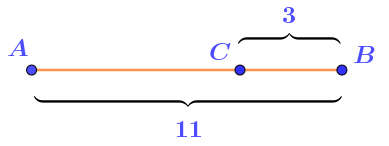
По правилу для расстояний между точками прямой можно записать равенство:
\(\displaystyle AC+BC=AB{\small .}\)
Подставляя данные задачи, получим:
\(\displaystyle AC+3=11\)
Откуда:
\(\displaystyle AC=\)\(\displaystyle 8{\small .}\)
Ответ: для искомой длины отрезка возможны значения \(\displaystyle 8\) и \(\displaystyle 14{\small .}\)