Skip to main content

Теория: 03 Длина отрезка при неопределённости расположения точек на прямой (короткая версия)

Скриншот экрана
  Скачать
Задание

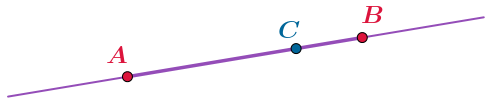
Сумма расстояний от точки \(\displaystyle C\) до концов отрезка \(\displaystyle AB\) длиной \(\displaystyle 5\) равна \(\displaystyle 13{\small .}\)

Какие значения может принимать длина отрезка \(\displaystyle AC{ \small ,}\) если точки \(\displaystyle A{\small ,\;}B\) и \(\displaystyle C\) принадлежат одной прямой?

Решение

Из трёх точек прямой ровно одна лежит между двумя другими.

Для этой точки можно использовать правило расстояний между точками прямой.

Разберём три случая, в которых на эту роль претендуют обозначения \(\displaystyle A{\small ,\;}B\) и \(\displaystyle C{\small .}\)

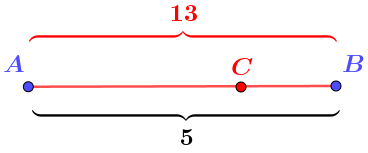
1. Точка \(\displaystyle C\) не может лежать между точками \(\displaystyle A\) и \(\displaystyle B{\small .}\)

В противном случае длина отрезка \(\displaystyle AB\) была бы равна сумме расстояний от точки \(\displaystyle C\) до точек \(\displaystyle A\) и \(\displaystyle B{ \small ,}\) то есть тринадцати.

Но по условию его длина равна \(\displaystyle 5 {\small .}\)

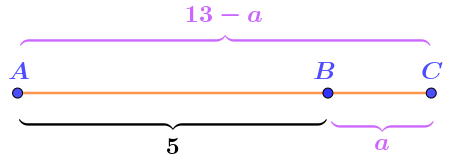
2. Пусть точка \(\displaystyle B\) лежит между точками \(\displaystyle A\) и \(\displaystyle C{\small .}\)

По правилу для расстояний между точками прямой можно записать равенство:

\(\displaystyle AB+BC=AC{\small .}\)

По условию \(\displaystyle AB=5{\small .} \)

Кроме того, сумма расстояний от точки \(\displaystyle C\) до концов отрезка \(\displaystyle AB\) равна \(\displaystyle 13{\small .}\) То есть

\(\displaystyle AC =13-BC{\small .}\)

Так как \(\displaystyle AC=AB+BC{ \small ,} \) то, подставляя, получаем:

\(\displaystyle AB+BC =13-BC{\small ,}\)

\(\displaystyle 5+2BC=13{\small ,}\)

\(\displaystyle 2BC=8{\small ,}\)

\(\displaystyle BC=4{\small .} \)

Значит, \(\displaystyle AC=AB+BC=5+4=\color{green}{ 9}{\small .}\)

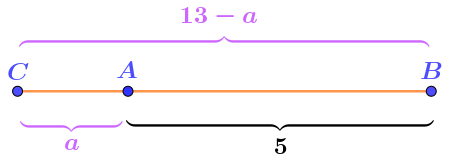
3. Пусть точка \(\displaystyle A\) лежит между точками \(\displaystyle B\) и \(\displaystyle C{\small .}\)

По правилу для расстояний между точками прямой можно записать равенство:

\(\displaystyle AB+AC=BC{\small .}\)

По условию \(\displaystyle AB=5{\small .} \)

Кроме того, сумма расстояний от точки \(\displaystyle C\) до концов отрезка \(\displaystyle AB\) равна \(\displaystyle 13{\small .}\) То есть

\(\displaystyle BC =13-AC{\small .}\)

Так как \(\displaystyle BC=AB+AC{ \small ,} \) то, подставляя, получаем:

\(\displaystyle AB+AC =13-AC{\small ,}\)

\(\displaystyle 5+2AC=13{\small ,}\)

\(\displaystyle 2AC=8{\small ,}\)

\(\displaystyle AC=\color{green}{ 4}{\small .}\)

Ответ: для искомой длины отрезка возможны значения \(\displaystyle 4\) и \(\displaystyle 9{\small .}\)