Точка \(\displaystyle M\) делит диагональ \(\displaystyle AC\) параллелограмма \(\displaystyle ABCD\) в отношении \(\displaystyle AM:MC=1:3\small.\)
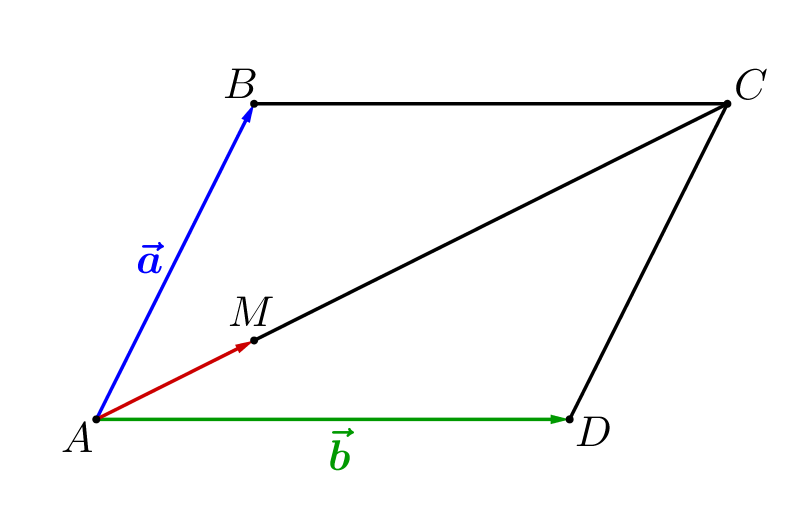
Обозначим векторы \(\displaystyle \overrightarrow{AB}=\vec{a}\) и \(\displaystyle \overrightarrow{AD}=\vec{b}\small.\) Разложите вектор \(\displaystyle \overrightarrow{AM}\) по векторам \(\displaystyle \vec{a}\) и \(\displaystyle \vec{b}\small.\)
По условию \(\displaystyle AM:MC=1:3\small.\) То есть \(\displaystyle AM=\frac{1}{4}AC\) и \(\displaystyle \overrightarrow{AM}=\frac{1}{4}\overrightarrow{AC}\small.\) Вектор \(\displaystyle \overrightarrow{AC}\) можно найти, используя правило треугольника: \(\displaystyle \overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}\small.\) Так как \(\displaystyle ABCD\)– параллелограмм, то \(\displaystyle \overrightarrow{BC}=\overrightarrow{AD}\small.\) Тогда вектор \(\displaystyle \overrightarrow{AC}\) можно представить как сумму векторов: \(\displaystyle \overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AB}+\overrightarrow{AD}=\color{blue}{\vec{a}}+\color{green}{\vec{b}}\small.\) Таким образом, получаем: \(\displaystyle \overrightarrow{AM}=\frac{1}{4}\overrightarrow{AC}=\frac{1}{4}(\color{blue}{\vec{a}}+\color{green}{\vec{b}})\small.\) | 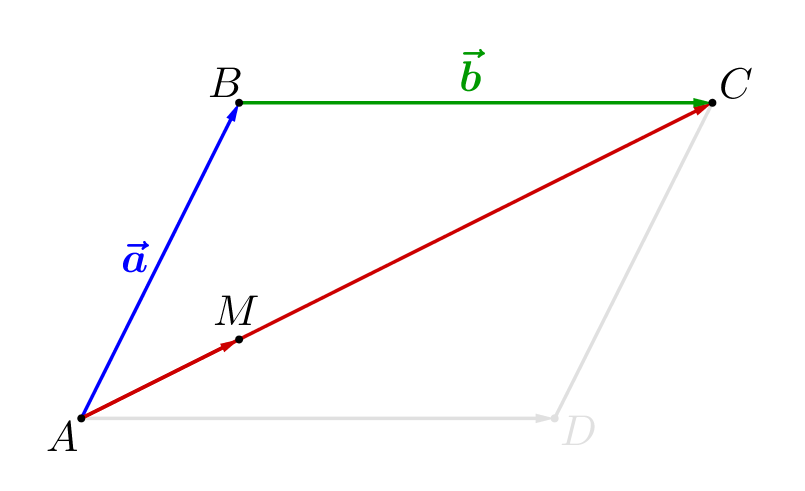 |