Координаты вершин треугольника \(\displaystyle ABC\) равны: \(\displaystyle A(-2;\,3),\,B(4;\,2),\,C(2;-1)\small.\) Напишите уравнение прямой, содержащей медиану \(\displaystyle AM{\small:}\)
(В каждом окне ввода укажите число.)
Чтобы решить задачу:
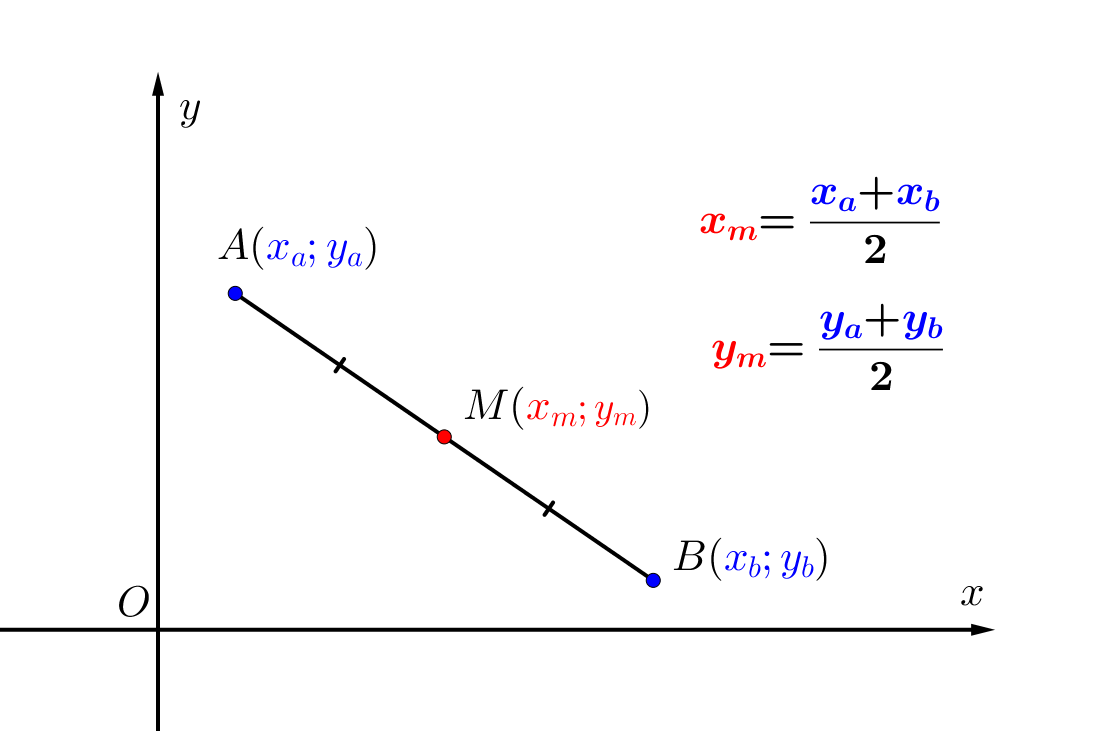
- найдем координаты точки \(\displaystyle M\small,\)
- найдем уравнение прямой, проходящей через точки \(\displaystyle A\) и \(\displaystyle M\small.\)
\(\displaystyle M\left(3;\frac{1}{2}\right)\small.\)
2. Найдем уравнение прямой, проходящей через точки \(\displaystyle A\) и \(\displaystyle M{\small.}\)
Уравнение любой прямой можно записать одним из двух способов:
- \(\displaystyle y=kx+b\small,\)
- \(\displaystyle x=x_0\small,\) если прямая вертикальная.
Точки \(\displaystyle A(-2;\,3)\) и \(\displaystyle M\left(3;\frac{1}{2}\right)\) имеют разные абсциссы. То есть прямая, проходящая через точки \(\displaystyle A\) и \(\displaystyle M\small,\) не вертикальная.
Тогда уравнение прямой \(\displaystyle AM\) можно записать в виде:
\(\displaystyle y=kx+b\small.\)
Последовательно подставляя координаты точек \(\displaystyle A\) и \(\displaystyle M\) в это уравнение, получаем систему из двух линейных уравнений:
\(\displaystyle \begin{cases}-2k+b=3,\\3k+b=\frac{1}{2}.\end{cases}\)
Решая эту систему, находим:
\(\displaystyle k=-\frac{1}{2}\) и \(\displaystyle b=2\small.\)
Тогда уравнение прямой:
\(\displaystyle y=-\frac{1}{2}x+2\small.\)
Или в общем виде:
\(\displaystyle \frac{1}{2}x+y-2=0\small,\)
\(\displaystyle x+2y-4=0\small.\)
Ответ: \(\displaystyle x+2y-4=0\small.\)