Определите, сколько точек пересечения имеют окружности, заданные уравнениями
\(\displaystyle x^2+(y+1)^2=4\) и \(\displaystyle x^2+y^2=16\small.\)
Если точка лежит и на первой, и на второй окружности, то для ее координат выполняются оба уравнения:
\(\displaystyle \begin{cases}x^2+(y+1)^2=4,\\x^2+y^2=16.\end{cases}\)
Решим систему уравнений и найдем координаты точек пересечения.
Вычтем из первого уравнения второе, чтобы избавиться от \(\displaystyle x{\small:}\)
\(\displaystyle \left(x^2+(y+1)^2\right)-\left(x^2+y^2\right)=4-16\small,\)
\(\displaystyle (y+1)^2-y^2=-12\small.\)
Раскроем скобки, используя формулу квадрата суммы, и упростим выражение:
\(\displaystyle y^2+2\cdot y\cdot1+1^2-y^2=-12\small,\)
\(\displaystyle 2y+1=-12\small,\)
\(\displaystyle y=-\frac{13}{2}\small.\)
Подставим \(\displaystyle y=-\frac{13}{2}\) во второе уравнение, чтобы найти \(\displaystyle x{\small:}\)
\(\displaystyle x^2+\left(-\frac{13}{2}\right)^2=16\small,\)
\(\displaystyle x^2=-\frac{105}{4}\small.\)
Квадрат всегда не меньше \(\displaystyle 0\small.\) То есть таких \(\displaystyle x\) не существует.
Значит, система решений не имеет.
Тогда нет ни одной точки на плоскости, которая лежит на обеих окружностях.
Ответ: \(\displaystyle 0\small.\)
Задачу можно решить геометрически. Изобразим окружности на рисунке:
- Синим цветом отметим окружность, заданную уравнением \(\displaystyle x^2+(y+1)^2=4\small.\) Ее центр – точка \(\displaystyle (0;\,-1)\) и радиус \(\displaystyle r=\sqrt{4}=2\small.\)
- Зеленым цветом отметим окружность, заданную уравнением \(\displaystyle x^2+y^2=16\small.\) Ее центр – точка \(\displaystyle (0;\,0)\) и радиус \(\displaystyle R=\sqrt{16}=4\small.\)
- Красным цветом отметим точки пересечения зеленой окружности с прямой, на которой расположены центры \(\displaystyle O\) и \(\displaystyle E\small.\)
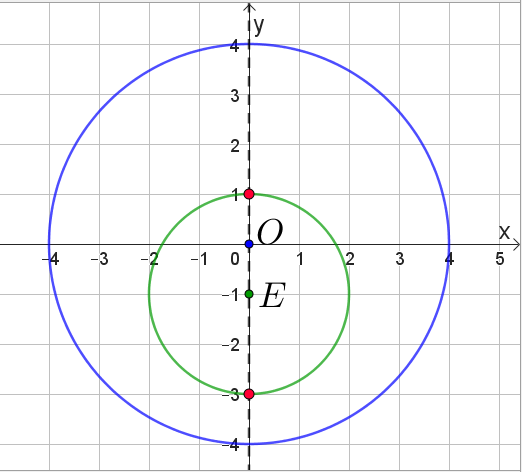
Обе красные точки находятся внутри синей окружности. Тогда вся зеленая окружность лежит внутри синей. То есть они не имеют точек пересечения.