Дан прямоугольник \(\displaystyle ABCD\) со сторонами \(\displaystyle AB=5\) и \(\displaystyle BC=7\small.\) Найдите множество всех точек \(\displaystyle M,\) для каждой из которых
\(\displaystyle AM^2+DM^2-BM^2-CM^2=2AB^2\small.\)
Введем прямоугольную систему координат так, чтобы
- сторона \(\displaystyle AD\) лежала на оси абсцисс,
- сторона \(\displaystyle AB\) лежала на оси ординат.
Напишите уравнение линии, которую образуют все такие точки \(\displaystyle M{\small:}\)
Сделаем рисунок к задаче. Тогда в прямоугольной системе координат на рисунке:
- точка \(\displaystyle A\) начало координат,
- стороны прямоугольника параллельны осям.
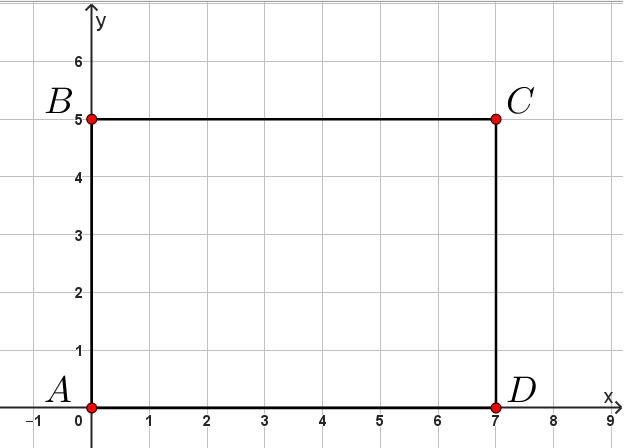
Тогда координаты точек: \(\displaystyle A(0;\,0),\,B(0;\,5),\,C(7;\,5),\,D(7;\,0)\small.\)
Пусть точка \(\displaystyle M \) имеет координаты \(\displaystyle (x;\,y)\small.\)
- \(\displaystyle AM^2=x^2+y^2\small,\)
- \(\displaystyle BM^2=x^2+(y-5)^2\small,\)
- \(\displaystyle CM^2=(x-7)^2+(y-5)^2\small,\)
- \(\displaystyle DM^2=(x-7)^2+y^2\small,\)
- \(\displaystyle AB^2=5^2=25\small.\)
Подставляя в выражение, предложенное в условии, получаем:
\(\displaystyle AM^2+DM^2-BM^2-CM^2=2AB^2{ \small ,}\\ \)
\(\displaystyle (\cancel{x^2}+y^2)+(\cancel{(x-7)^2}+y^2)-(\cancel{x^2}+(y-5)^2)-(\cancel{(x-7)^2}+(y-5)^2)=2\cdot 25\small.\)
Упростив выражение, получаем:
\(\displaystyle y^2+y^2-(y-5)^2-(y-5)^2=50\small.\)
\(\displaystyle y=5\small.\)
Таким образом, все точки \(\displaystyle M\) из условия лежат на прямой, заданной уравнением
\(\displaystyle y=5\small.\)
Ответ: \(\displaystyle y=5\small.\)