Дан ромб \(\displaystyle ABCD\small,\) диагонали которого равны \(\displaystyle 6\) и \(\displaystyle 8\small.\) Найдите множество всех точек \(\displaystyle M\small,\) для каждой из которых
\(\displaystyle AM^2+DM^2=BM^2+CM^2\small.\)
Выберите верный ответ:
Диагонали ромба перпендикулярны и делятся точкой пересечения пополам.
Тогда введем прямоугольную систему координат так, чтобы
- диагональ \(\displaystyle AC\) лежала на оси абсцисс,
- диагональ \(\displaystyle BD\) лежала на оси ординат.
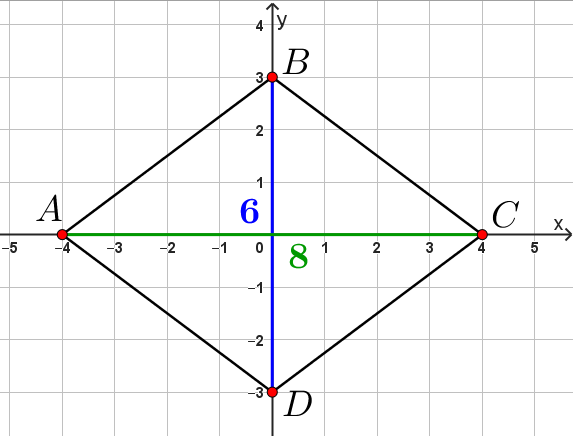
В этом случае координаты точек: \(\displaystyle A(-4;\,0),\,B(0;\,3),\,C(4;\,0),\,D(0;\,-3)\small.\)
Пусть точка \(\displaystyle M \) имеет координаты \(\displaystyle (x;\,y)\small.\)
- \(\displaystyle AM^2=(x+4)^2+y^2\small,\)
- \(\displaystyle BM^2=x^2+(y-3)^2\small,\)
- \(\displaystyle CM^2=(x-4)^2+y^2\small,\)
- \(\displaystyle DM^2=x^2+(y+3)^2\small.\)
Подставляя в выражение \(\displaystyle AM^2+DM^2=BM^2+CM^2\small,\) предложенное в условии, получаем:
\(\displaystyle (x+4)^2+\cancel{y^2}+\cancel{x^2}+(y+3)^2=\cancel{x^2}+(y-3)^2+(x-4)^2+\cancel{y^2}\small.\)
Упростив выражение, получаем:
\(\displaystyle (x+4)^2+(y+3)^2=(y-3)^2+(x-4)^2\small.\)
\(\displaystyle y=-\frac{4}{3}x\small.\)
Таким образом, все точки \(\displaystyle M\) из условия лежат на прямой, заданной уравнением
\(\displaystyle y=-\frac{4}{3}x\small.\)
Определим, является ли эта прямая параллельной или перпендикулярной одной из сторон. Для этого вычислим угловые коэффициенты прямых, содержащих стороны ромба:
\(\displaystyle y=\frac{3}{4}x+3\small.\)
\(\displaystyle y=-\frac{3}{4}x+3\small.\)
Ни у одной из прямых, содержащих стороны ромба, угловой коэффициент не совпадает с угловым коэффициентом прямой \(\displaystyle y=-\frac{4}{3}x\small.\) Значит, среди этих прямых нет параллельных.
Заметим, что
\(\displaystyle -\frac{4}{3} \cdot \frac{3}{4} = -1\small.\)
Тогда прямая \(\displaystyle y=-\frac{4}{3}x\) перпендикулярна прямой \(\displaystyle y=\frac{3}{4}x+3\small.\)
Таким образом, все точки \(\displaystyle M\) образуют прямую, проходящую через центр ромба и перпендикулярную стороне \(\displaystyle AB\small.\)
Ответ: Все точки \(\displaystyle M\) образуют прямую, проходящую через центр ромба и перпендикулярную стороне \(\displaystyle AB\small.\)
Если изменить положение ромба относительно координатных осей, то уравнение искомой прямой будет другим. Однако это всегда будет прямая, проходящая через центр ромба и перпендикулярная стороне \(\displaystyle AB\small.\)