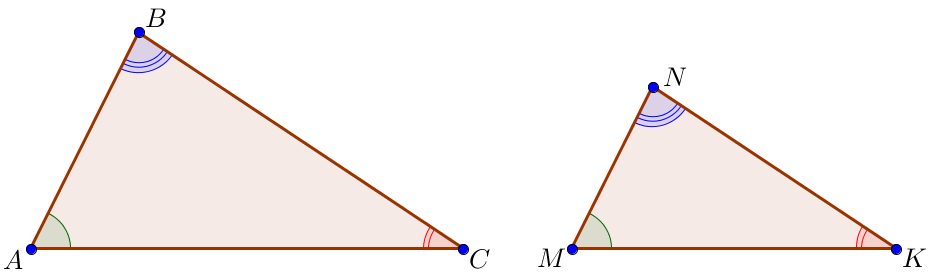
Решите задачу на готовом чертеже:
Треугольники \(\displaystyle ABC\) и \(\displaystyle A_1B_1C_1\) подобны: \(\displaystyle \angle A=\angle A_1{\small,}\) \(\displaystyle \angle B=\angle B_1{\small,}\) \(\displaystyle \angle C=\angle C_1{\small.}\)
По данному рисунку найдите значения \(\displaystyle x{\small,}\) \(\displaystyle y{\small,}\) \(\displaystyle z{\small, }\) если известно, что \(\displaystyle \frac{AC}{A_1C_1}=2{\small.}\)
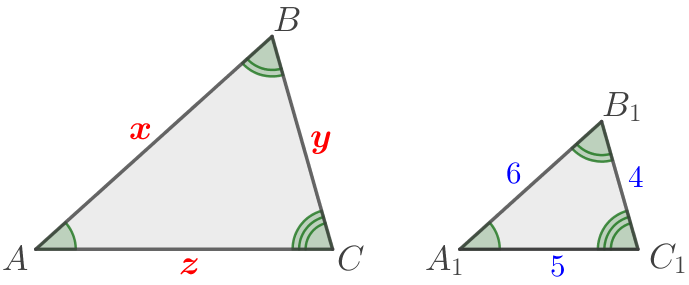
\(\displaystyle x=\)\(\displaystyle {\small;}\) \(\displaystyle y=\)\(\displaystyle {\small;}\) \(\displaystyle z=\)\(\displaystyle {\small.}\)
\(\displaystyle \triangle ABC \sim \triangle A_1B_1C_1\) и \(\displaystyle \frac{AC}{A_1C_1}=2{\small.}\)

В подобных треугольниках сходственные стороны лежат напротив соответственно равных углов.
Следовательно,
\(\displaystyle \frac{AB}{A_1B_1}=\frac{BC}{B_1C_1}=\frac{AC}{A_1C_1}=2{\small.}\)
То есть
\(\displaystyle \frac{x}{6}=\frac{y}{4}=\frac{z}{5}=2{\small.}\)
Тогда
\(\displaystyle x=12{\small;}\)
\(\displaystyle y=8{\small;}\)
\(\displaystyle z=10{\small.}\)
Ответ: \(\displaystyle x=12{\small;}\) \(\displaystyle y=8{\small;}\) \(\displaystyle z=10{\small.}\)