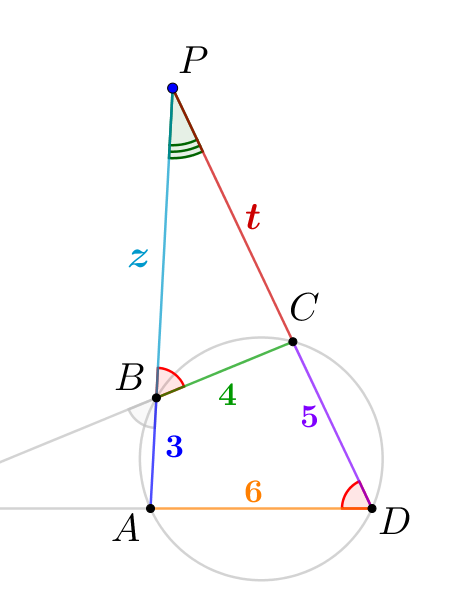
Дан вписанный в окружность четырёхугольник \(\displaystyle ABCD\) со сторонами \(\displaystyle AB = 3,\, BC = 4,\, CD = 5,\, DA = 6.\) Продолжения сторон \(\displaystyle AB\) и \(\displaystyle CD\) пересекаются в точке \(\displaystyle P\small,\) а продолжения сторон \(\displaystyle BC\) и \(\displaystyle DA\) – в точке \(\displaystyle Q\small.\) Найдите сумму длин отрезков \(\displaystyle QA\) и \(\displaystyle PC\small.\) \(\displaystyle QA+PC=\) |
У вписанного четырехугольника сумма противоположных углов равна \(\displaystyle 180^{\circ}\small.\) Тогда отметим равные углы на картинке:
Все три угла \(\displaystyle \angle QBA,\,\angle PBC\) и \(\displaystyle \angle ADC\) равны \(\displaystyle 180^{\circ}-\angle ABC\small.\)
Тогда есть две пары треугольников, подобных по двум углам (один угол общий):
- \(\displaystyle \triangle BQA\thicksim\triangle DCQ\small,\)
- \(\displaystyle \triangle BPC\thicksim\triangle DPA\small.\)
\(\displaystyle QA=\frac{57}{8}\small.\)
Поскольку треугольники \(\displaystyle BQA\) и \(\displaystyle DCQ\) подобны, то равны отношения соответственных сторон: \(\displaystyle \frac{QB}{QD}=\frac{QA}{QC}=\frac{AB}{CD}\small.\) Обозначим \(\displaystyle QB=x\) и \(\displaystyle QA=y\small.\) Подставляя известные длины сторон, получаем: \(\displaystyle \frac{x}{y+6}=\frac{y}{x+4}=\frac{3}{5}\small.\)
| 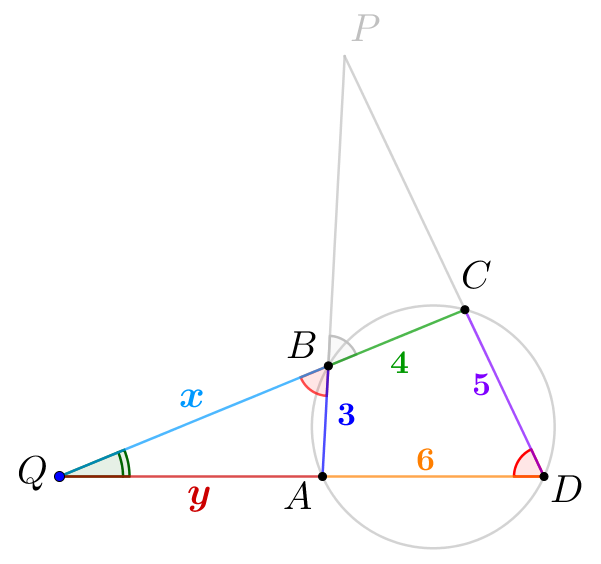 |
Тогда имеем систему из двух линейных уравнений:
\(\displaystyle \begin{cases}x=\frac{3}{5}(y+6),\\y=\frac{3}{5}(x+4).\end{cases}\)
Подставим \(\displaystyle x=\frac{3}{5}(y+6)\) во второе уравнение и найдем \(\displaystyle y{\small:}\)
\(\displaystyle y=\frac{3}{5}\left(\frac{3}{5}(y+6)+4\right)\small,\)
\(\displaystyle y=\frac{9}{25}y+\frac{114}{25}\small,\)
\(\displaystyle 16y=114\small,\)
\(\displaystyle y=\frac{57}{8}\small.\)
То есть
\(\displaystyle QA=y=\frac{57}{8}\small.\)
\(\displaystyle PC=\frac{38}{5}\small.\)
Таким образом
\(\displaystyle QA+PC=\frac{57}{8}+\frac{38}{5}=\frac{589}{40}\small.\)
Ответ: \(\displaystyle QA+PC=\frac{589}{40}\small.\)