В четырехугольнике \(\displaystyle ABCD\) диагонали перпендикулярны. Точка пересечения диагоналей делит их на части \(\displaystyle a,\,b,\,c,\,d\) (как показано на рисунке).
Выразите суммы квадратов противоположных сторон через \(\displaystyle a,\,b,\,c,\,d{\small:}\)
Что можно сказать про суммы квадратов противоположных сторон четырехугольника \(\displaystyle ABCD?\)
Обозначим точку пересечения диагоналей буквой \(\displaystyle O{\small.}\)
Взаимно перпендикулярные диагонали \(\displaystyle AC\) и \(\displaystyle BD\) разбивают четырёхугольник \(\displaystyle ABCD\) на четыре прямоугольных треугольника:
\(\displaystyle \triangle AOB,\,\triangle BOC,\,\triangle COD,\,\triangle DOA\small.\)
По теореме Пифагора в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
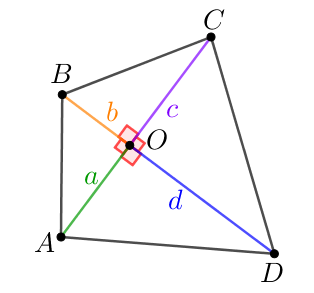 | Запишем теорему Пифагора для каждого из четырех прямоугольных треугольников:
|
Найдём суммы квадратов противоположных сторон четырёхугольника \(\displaystyle ABCD{\small:}\)
\(\displaystyle AB^2+CD^2=a^2+b^2+c^2+d^2\small,\)
\(\displaystyle BC^2+DA^2=b^2+c^2+d^2+a^2\small.\)
В обоих выражениях квадрат каждой из переменных \(\displaystyle a,\,b,\,c,\,d\) встречается ровно один раз.
То есть суммы квадратов противоположных сторон четырехугольника \(\displaystyle ABCD\) равны.
| Ответ: | \(\displaystyle AB^2+CD^2=a^2+b^2+c^2+d^2\) \(\displaystyle BC^2+DA^2=a^2+b^2+c^2+d^2\) Суммы квадратов противоположных сторон четырехугольника \(\displaystyle ABCD\) равны. |