Две стороны треугольника равны \(\displaystyle 14\) и \(\displaystyle 18\small.\) Медианы, проведенные к этим сторонам, взаимно перпендикулярны. Найдите третью сторону треугольника.
Пусть \(\displaystyle ABC\) – треугольник:
\(\displaystyle AM=BM=14:2=7\small,\) \(\displaystyle BN=CN=18:2=9\small;\)
| 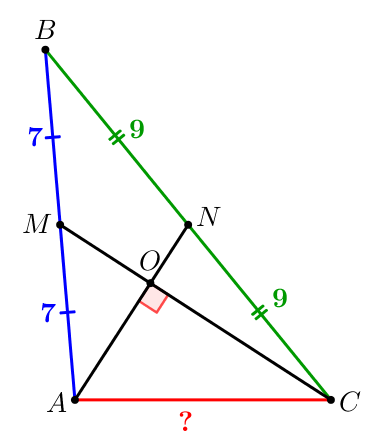 |
Требуется найти длину \(\displaystyle AC{\small.}\)
Рассмотрим четырехугольник \(\displaystyle MNCA\small:\) \(\displaystyle \color{red}{1)}\) сторона \(\displaystyle MN\) является средней линией треугольника \(\displaystyle ABC\small.\) Следовательно, \(\displaystyle MN=\frac{AC}{2}\small.\) Обозначим \(\displaystyle MN=x\small,\) тогда \(\displaystyle AC=2x\small.\) | 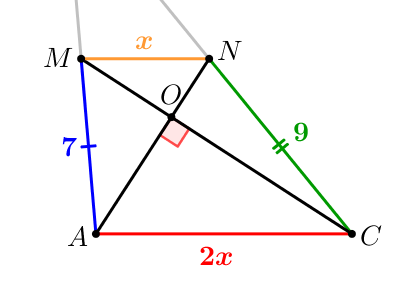 |
\(\displaystyle \color{red}{2)}\) диагонали \(\displaystyle AN\) и \(\displaystyle CM\) четырёхугольника \(\displaystyle MNCA\) взаимно перпендикулярны. Значит,
\(\displaystyle AM^2+CN^2=AC^2+MN^2\small.\)
Подставим известные значения:
\(\displaystyle \color{blue}7^2+\color{green}9^2=\color{orange}x^2+(\color{red}{2x})^2\small.\)
Упростим выражение и найдем \(\displaystyle x\small:\)
\(\displaystyle 130=5x^2\small;\)
\(\displaystyle x^2=26{\small.}\)
\(\displaystyle x\) – длина отрезка, значит, \(\displaystyle x>0{\small:}\)
\(\displaystyle x=\sqrt{26}\small.\)
Найдём \(\displaystyle AC{\small:}\)
\(\displaystyle AC=2x=2\sqrt{26}\small.\)
Ответ: \(\displaystyle 2\sqrt{26}\small.\)