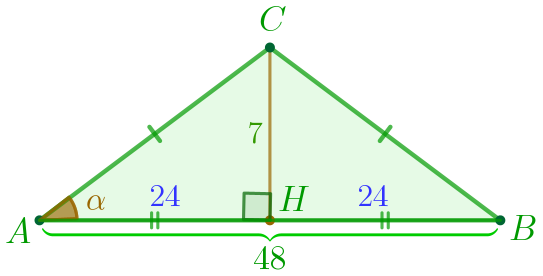
В треугольнике \(\displaystyle ABC\) известно, что \(\displaystyle AC=BC{\small , }\) высота \(\displaystyle CH=7\) и \(\displaystyle AB=48{\small .}\) Найдите \(\displaystyle \sin\angle BAC.\)
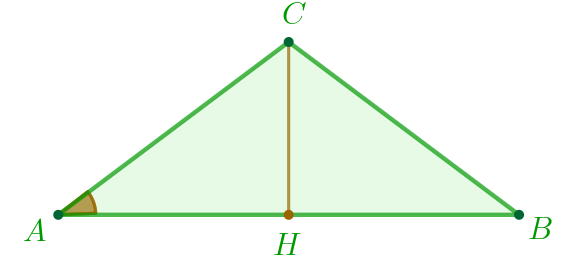
Пусть\(\displaystyle AB=48 {\small,}\) \(\displaystyle CH=7{\small .}\)
Треугольник \(\displaystyle ABC\) равнобедренный. Следовательно, \(\displaystyle CH{\small }\) – высота и медиана. Значит, \(\displaystyle AH=HB=48:2=24{\small.}\) |
|
Найдём \(\displaystyle \sin\angle BAC\) из прямоугольного треугольника \(\displaystyle AHC{\small:}\)
В треугольнике \(\displaystyle AHC{\small :}\)
Воспользуемся теоремой Пифагора\(\displaystyle {\small:}\) \(\displaystyle CH^2+AH^2=AC^2{\small .}\) Получаем: \(\displaystyle 7^2+24^2=AC^2{\small .}\) Значит, \(\displaystyle AC^2=49+576=625{\small .}\) Так как длина отрезка положительна, \(\displaystyle AC=25{\small .}\) | 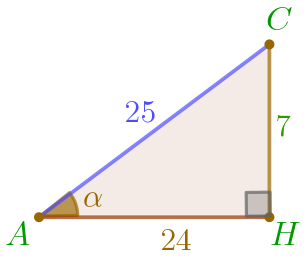 |
По определению
\(\displaystyle \sin \alpha=\frac{CH}{AC}{\small.}\)
Получаем:
\(\displaystyle \sin \alpha=\frac{7}{25}{\small.}\)
Значит,
\(\displaystyle \sin\angle BAC=0{,}28{\small .}\)
Ответ: \(\displaystyle 0{,}28{\small .}\)