Решить систему графически:
\(\displaystyle\begin{aligned}\begin{cases}3x+2y=-5{\small,}\\2x+3y=-10{\small.}\\\end{cases}\\\end{aligned}\)
Двигая синие точки, постройте график одного уравнения. Двигая зелёные точки, постройте график другого уравнения.
По полученному рисунку определите решение системы уравнений.
\(\displaystyle x=\) \(\displaystyle ,\) \(\displaystyle y=\) \(\displaystyle .\)
\(\displaystyle \color{blue}{(-1;-1)}\) и \(\displaystyle \color{blue}{(3;-7)}{\small.}\)
\(\displaystyle \color{green}{(-2;-2)}\) и \(\displaystyle \color{green}{(4;-6)}{\small.}\)
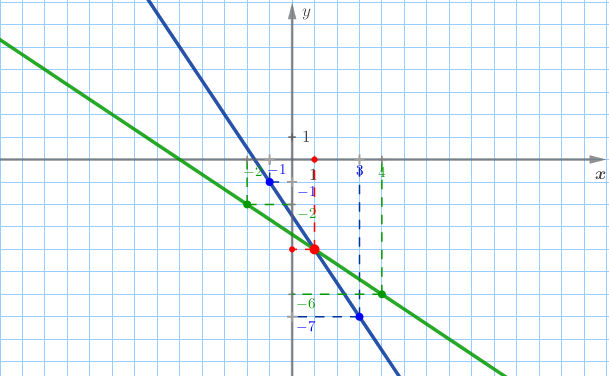
На рисунке точка пересечения прямых выделена красным цветом.
Координаты этой точки удовлетворяют как первому уравнению, так и второму, то есть являются решением системы:
\(\displaystyle\begin{aligned}\begin{cases}3x+2y=-5{\small,}\\2x+3y=-10{\small.}\\\end{cases}\\\end{aligned}\)
Определим по рисунку координаты точки пересечения:
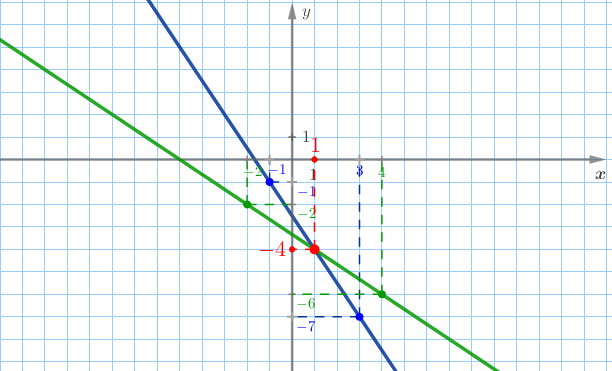
Прямые пересекаются в точке \(\displaystyle \color{red}{(1;-4)}{\small.}\) Значит, система имеет единственное решение:
\(\displaystyle x=1{\small,}\) \(\displaystyle y=-4{\small.}\)
Ответ: \(\displaystyle x=1{\small,}\) \(\displaystyle y=-4{\small.}\)