График уравнения \(\displaystyle 7x+6y=42\) пересекает ось ординат в точке \(\displaystyle A(x_{_1};y_{_1}){\small,}\) ось абсцисс – в точке \(\displaystyle B(x_{_2};y_{_2}){\small.}\) Найдите координаты точек \(\displaystyle A\) и \(\displaystyle B{\small.}\)
\(\displaystyle A\bigg(\) \(\displaystyle ;\) \(\displaystyle \bigg)\)
\(\displaystyle B\bigg(\) \(\displaystyle ;\) \(\displaystyle \bigg)\)
Двигая по оси ординат красную точку \(\displaystyle A\) и по оси абсцисс синюю точку \(\displaystyle B{\small,}\) постройте график уравнения \(\displaystyle 7x+6y=42{\small.}\)
По полученному рисунку сформулируйте верное утверждение:
График уравнения расположен в
\(\displaystyle \color{red}{1.}\) Найдём координаты точки \(\displaystyle A{\small.}\)
Точка \(\displaystyle A(x_{_1};y_{_1})\) принадлежит графику уравнения \(\displaystyle 7x+6y=42{\small,}\) следовательно
\(\displaystyle 7\cdot x_{_1}+6\cdot y_{_1}=42{\small.}\)
\(\displaystyle A(x_{_1};y_{_1})\) – точка пересечения графика уравнения \(\displaystyle 7x+6y=42\) с оcью ординат. Значит,
\(\displaystyle x_{_1}=0{\small.}\)
Тогда
\(\displaystyle y_{_1}=7{\small.}\)
В результате получаем
\(\displaystyle A(0\ ;\ 7){\small.}\)
\(\displaystyle \color{red}{2.}\) Найдём координаты точки \(\displaystyle B{\small.}\)
Точка \(\displaystyle B(x_{_2};y_{_2})\) принадлежит графику уравнения \(\displaystyle 7x+6y=42{\small,}\) следовательно
\(\displaystyle 7\cdot x_{_2}+6\cdot y_{_2}=42{\small.}\)
\(\displaystyle B(x_{_2};y_{_2})\) – точка пересечения графика уравнения \(\displaystyle 7x+6y=42\) с оcью абсцисс. Значит,
\(\displaystyle y_{_2}=0{\small.}\)
Тогда
\(\displaystyle x_{_2}=6{\small.}\)
В результате получаем
\(\displaystyle B(6\ ;\ 0 ){\small.}\)
\(\displaystyle \color{red}{3.}\) Построим график уравнения.
Графиком линейного уравнения \(\displaystyle 7x+6y=42\) служит прямая, проходящая через точки \(\displaystyle A(0\ ;\ 7)\) и \(\displaystyle B(6\ ;\ 0 ){\small.}\)
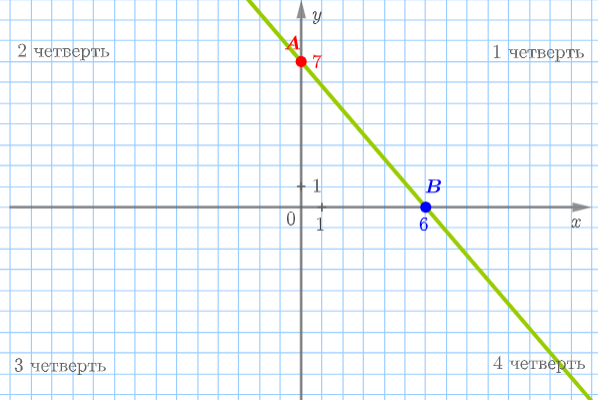
По рисунку видим, что прямая \(\displaystyle AB\) расположена в \(\displaystyle 1{\small,}\) \(\displaystyle 2{\small,}\) \(\displaystyle 4\) координатных четвертях.
| Ответ: | \(\displaystyle A(0\ ;\ 7){\small,}\) \(\displaystyle B(6\ ;\ 0 ){\small.}\) |
| График уравнения расположен в \(\displaystyle 1{\small,}\) \(\displaystyle 2{\small,}\) \(\displaystyle 4\) координатных четвертях. |